3.2. 이산 푸리에 변환 & 고속 푸리에 변환 (DFT & FFT)

Discrete Fourier Transform & Fast Fourier Transform

푸리에변환
FFT
Author

Cheonghyo Cho

Published

February 15, 2023

이산 푸리에 변환(DFT)과 그 기본 속성과 함께, DFT를 평가하는 효율적인 알고리즘인 고속 푸리에 변환(FFT)을 소개한다.

이 글은 FMP(Fundamentals of Music Processing) Notebooks을 참고로 합니다.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import librosa
import scipy
import librosa
import IPython.display as ipd
# 푸리에 변환에 대한 시각화 설명
ipd.display(ipd.YouTubeVideo("spUNpyF58BY", width=16*40, height=9*40))
# FFT에 대한 한국어 설명
ipd.display(ipd.YouTubeVideo("eKSmEPAEr2U", width=16*40, height=9*40))

이산 푸리에 변환 (Discrete Fourier Transform, DFT)

내적 (Inner Product)

  • 푸리에 변환(Fourier transform)을 이해하기 위한 중요한 개념으로 \(N \in \mathbb{N}\)에 대한 복소(complex) 벡터 공간 \(\mathbb{C}^N\)에 대한 내적(inner product) 이 있다.

  • 두 개의 복소수 벡터 \(x, y \in \mathbb{C}^N\)가 주어지면, \(x\)와 \(y\) 사이의 내적은 다음과 같이 정의된다. \[\langle x | y \rangle := \sum_{n=0}^{N-1} x(n) \overline{y(n)}.\]

  • 내적의 절대값은 \(x\)와 \(y\) 사이의 유사성의 척도로 해석될 수 있다.

    • \(x\)와 \(y\)가 동일한 방향을 가리키면(즉, \(x\)와 \(y\)가 유사함), 내적 \(|\langle x | y \rangle|\)이 크다.
    • \(x\)와 \(y\)가 직교하면(즉, \(x\)와 \(y\)가 서로 다른 경우), 내적 \(|\langle x | y \rangle|\)는 0이다.

  • 함수 np.vdot을 사용하여 내적을 계산할 때 첫 번째 인수에 대해 복소 켤레(complex conjugate)가 수행된다는 점에 유의하자.

  • 따라서, 위에서 정의된 \(\langle x | y \rangle\)를 계산하려면, np.vdot(y, x)를 사용해야 한다.

x = np.array([ 1.0, 1j, 1.0 + 1.0j ])
y = np.array([ 1.1, 1j, 0.9 + 1.1j ])
print('Vectors of high similarity:', np.abs(np.vdot(y, x)))

x = np.array([ 1.0,   1j, 1.0 + 1j ])
y = np.array([ 1.1, -1j, 0.1      ])
print('Vectors of low similarity:', np.abs(np.vdot(y, x)))
Vectors of high similarity: 4.104875150354758
Vectors of low similarity: 0.22360679774997913

DFT의 정의

  • \(x\in \mathbb{C}^N\)을 길이가 \(N\in\mathbb{N}\)인 벡터라고 하자. 음악 신호의 맥락에서 \(x\)는 샘플 \(x(0), x(1), ..., x(N-1)\)가 있는 이산(discrete) 신호로 해석될 수 있다.

  • 이산 푸리에 변환(DFT)은 다음과 같이 정의된다. \[ X(k) := \sum_{n=0}^{N-1} x(n) \exp(-2 \pi i k n / N) \] for \(k \in [0:N-1]\).

  • 벡터 \(X\in\mathbb{C}^N\)는 시간 영역(time-domain) 신호 \(x\)의 주파수 표현(frequency representation)으로 해석될 수 있다.

  • DFT의 기하학적 해석을 얻기 위해 벡터 \(\mathbf{u}_k\in\mathbb{C}^N\)를 다음과 같이 정의한다. \[\mathbf{u}_k(n) := \exp(2 \pi i k n / N) = \cos(2 \pi k n / N) + i \sin(2 \pi k n / N)\] for \(k \in [0:N-1]\).

  • 이 벡터는 주파수 \(k/N\)의 지수 함수의 샘플링된 버전으로 볼 수 있다. 그러면 DFT는 신호 \(x\) 및 샘플링된 지수 함수 \(\mathbf{u}_k\)의 내적으로 표현될 수 있다. \[ X(k) := \sum_{n=0}^{N-1} x(n) \overline{\mathbf{u}_k} = \langle x | \mathbf{u}_k \rangle\]

  • 절대값 \(|X(k)|\)는 신호 \(x\)와 \(\mathbf{u}_k\) 사이의 유사도를 나타낸다.

  • \(x\in \mathbb{R}^N\)이 실수 값 벡터(음악 신호 시나리오의 경우, 항상 해당)인 경우 다음을 얻는다.

\[ X(k) := \langle x |\mathrm{Re}(\mathbf{u}_k) \rangle - i\langle x | \mathrm{Im}(\mathbf{u}_k) \rangle \]

  • 다음 그림은 두 개의 서로 다른 주파수 파라미터 \(k\)에 대한 함수 \(\overline{\mathbf{u}_k}\)와 비교한 신호 \(x\)의 예를 보여준다.
    • \(\overline{\mathbf{u}_k}\)의 실수부와 허수부는 각각 빨간색 및 파란색으로 표시된다.
N = 64
n = np.arange(N)
k = 3
x = np.cos(2 * np.pi * (k * n / N) + (1.2*np.random.rand(N) - 0.0))

plt.figure(figsize=(6, 4))

plt.subplot(2, 1, 1)
plt.plot(n, x, 'k', marker='.', markersize='5', linewidth=2.0, label='$x$')
plt.xlabel('Time (samples)')
k = 3
u_k_real = np.cos(2 * np.pi * k * n / N)
u_k_imag = -np.sin(2 * np.pi * k * n / N)
u_k = u_k_real + u_k_imag*1j
sim_complex = np.vdot(u_k, x)
sim_abs = np.abs(sim_complex)
plt.title(r'Signal $x$ and some $u_k$ (k=3) having high similarity: Re($X(k)$) = %0.2f, Im($X(k)$) = %0.2f,  $|X(k)|$=%0.2f'%(sim_complex.real,sim_complex.imag,sim_abs))
plt.plot(n, u_k_real, 'r', marker='.', markersize='3', 
         linewidth=1.0, linestyle=':', label='$\mathrm{Re}(\overline{\mathbf{u}}_k)$');
plt.plot(n, u_k_imag, 'b', marker='.', markersize='3', 
         linewidth=1.0, linestyle=':', label='$\mathrm{Im}(\overline{\mathbf{u}}_k)$');
plt.legend()

plt.subplot(2, 1, 2)
plt.plot(n, x, 'k', marker='.', markersize='5', linewidth=2.0, label='$x$')
plt.xlabel('Time (samples)')
k = 5
u_k_real = np.cos(2 * np.pi * k * n / N)
u_k_imag = -np.sin(2 * np.pi * k * n / N)
u_k = u_k_real + u_k_imag*1j
sim_complex = np.vdot(u_k, x)
sim_abs = np.abs(sim_complex)
plt.title(r'Signal $x$ and some $u_k$ (k=5) having low similarity: Re($X(k)$) = %0.2f, Im($X(k)$) = %0.2f,  $|X(k)|$=%0.2f'%(sim_complex.real,sim_complex.imag,sim_abs))
plt.plot(n, u_k_real, 'r', marker='.', markersize='3', 
         linewidth=1.0, linestyle=':', label='$\mathrm{Re}(\overline{\mathbf{u}}_k)$');
plt.plot(n, u_k_imag, 'b', marker='.', markersize='3', 
         linewidth=1.0, linestyle=':', label='$\mathrm{Im}(\overline{\mathbf{u}}_k)$');
plt.legend()

plt.tight_layout()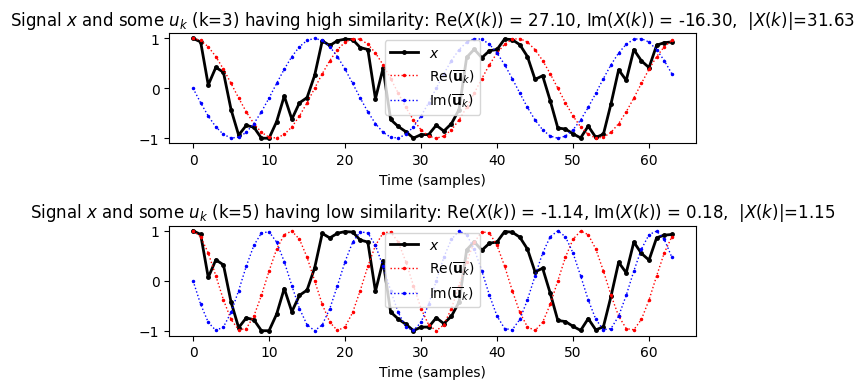

DFT 행렬 (DFT Matrix)

  • 선형 연산자 \(\mathbb{C}^N \to \mathbb{C}^N\)이면, DFT는 \(N\times N\)-행렬로 표현할 수 있다. 이는 다음과 같은 유명한 DFT 행렬 \(\mathrm{DFT}_N \in \mathbb{C}^{N\times N}\) 행렬로 이어진다. \[\mathrm{DFT}_N(n, k) = \mathrm{exp}(-2 \pi i k n / N)\] for \(n\in[0:N-1]\) and \(k\in[0:N-1]\).

  • \(\rho_N:=\exp(2 \pi i / N)\)를 단위 N승근 (primitive Nth roots of unity)이라고 한다. 또한 단위 N승근을 다음과 같이 정의한다.

    • \(\sigma_N:= \overline{\rho_N} = \mathrm{exp}(-2 \pi i / N)\)

  • 지수 함수의 속성으로부터 다음을 얻을 수 있다.

    • \(\sigma_N^{kn} = \mathrm{exp}(-2 \pi i / N)^{kn} = \mathrm{exp}(-2 \pi i k n / N)\)

  • 이로부터 다음의 행렬을 얻는다. \[ \mathrm{DFT}_N = \begin{pmatrix} 1 & 1 & 1 & \dots & 1 \\ 1 & \sigma_N & \sigma_N^2 & \dots & \sigma_N^{N-1} \\ 1 & \sigma_N^2 & \sigma_N^4 & \dots & \sigma_N^{2(N-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \sigma_N^{N-1} & \sigma_N^{2(N-1)} & \dots & \sigma_N^{(N-1)(N-1)} \\ \end{pmatrix} \]

  • 다음 그림에서 \(\mathrm{DFT}_N\)의 실수 및 허수 부분이 표시되며, 값은 적절한 색상으로 인코딩된다. \(\mathrm{DFT}_N\)의 \(k^\mathrm{th}\) 행은 위에 정의된 벡터 \(\mathbf{u}_k\)에 해당한다.

def generate_matrix_dft(N, K):
    """Generates a DFT (discrete Fourier transfrom) matrix

    Args:
        N (int): Number of samples
        K (int): Number of frequency bins

    Returns:
        dft (np.ndarray): The DFT matrix
    """
    dft = np.zeros((K, N), dtype=np.complex128)
    for n in range(N):
        for k in range(K):
            dft[k, n] = np.exp(-2j * np.pi * k * n / N)
    return dft

def dft(x):
    """Compute the disrcete Fourier transfrom (DFT)

    Args:
        x (np.ndarray): Signal to be transformed

    Returns:
        X (np.ndarray): Fourier transform of x
    """
    x = x.astype(np.complex128)
    N = len(x)
    dft_mat = generate_matrix_dft(N, N)
    return np.dot(dft_mat, x)
N = 32
dft_mat = generate_matrix_dft(N, N)

plt.figure(figsize=(10, 3))

plt.subplot(1, 2, 1)
plt.title('$\mathrm{Re}(\mathrm{DFT}_N)$')
plt.imshow(np.real(dft_mat), origin='lower', cmap='seismic', aspect='equal')
plt.xlabel('Time index $n$')
plt.ylabel('Frequency index $k$')
plt.colorbar()

plt.subplot(1, 2, 2)
plt.title('$\mathrm{Im}(\mathrm{DFT}_N)$')
plt.imshow(np.imag(dft_mat), origin='lower', cmap='seismic', aspect='equal')
plt.xlabel('Time index $n$')
plt.ylabel('Frequency index $k$')
plt.colorbar()
plt.tight_layout()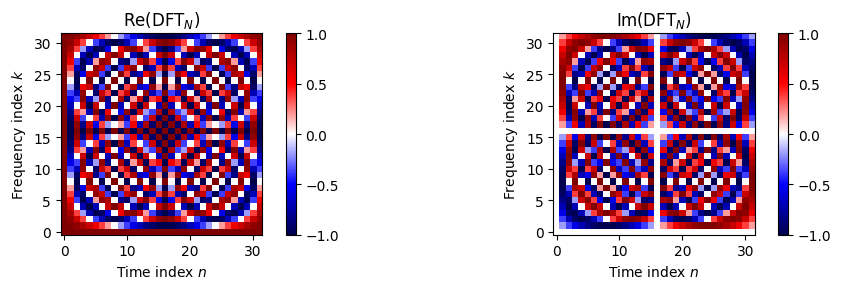

N = 128
n = np.arange(N)
k = 10
x = np.cos(2 * np.pi * (k * n / N) + 2 * (np.random.rand(N) - 0.5)) 
X = dft(x)

plt.figure(figsize=(8, 3))

plt.subplot(1, 2, 1)
plt.title('$x$')
plt.plot(x)
plt.xlabel('Time (index $n$)')

plt.subplot(1, 2, 2)
plt.title('$|X|$')
plt.plot(np.abs(X))
plt.xlabel('Frequency (index $k$)')
plt.tight_layout()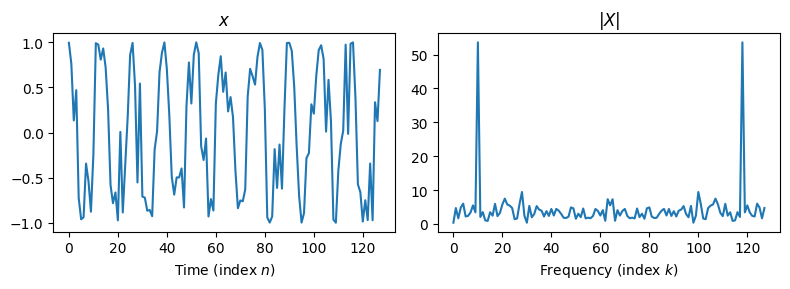

고속 푸리에 변환 (Fast Fourier Transform, FFT)

  • 다음으로 DFT를 계산하는 빠른 알고리즘인 고속 푸리에 변환(FFT)에 대해 설명한다. FFT 알고리즘은 원래 1805년 즈음에 Gauss에 의해 발견되었고 1965년에 Cooley와 Tukey에 의해 재발견되었다.

  • FFT 알고리즘은 짝수 크기 \(N=2M\)의 DFT를 적용하는 것이 \(M\)의 절반 크기인 두 개의 DFT를 적용하는 것으로 표현될 수 있다는 관찰을 기반으로 한다. DFT 행렬의 \(\sigma_N^{kn} = \mathrm{exp}(-2 \pi i / N)^{kn}\) 항목 사이에 대수 관계가 있다는 사실을 이용한다.

\[\sigma_M = \sigma_N^2\]

  • FFT 알고리즘에서 \(x\)의 짝수-인덱스와 홀수-인덱스 항목의 DFT를 계산한다. \[\begin{align} (A(0), \dots, A(N/2-1)) &= \mathrm{DFT}_{N/2} \cdot (x(0), x(2), x(4), \dots, x(N-2))\\ (B(0), \dots, B(N/2-1)) &= \mathrm{DFT}_{N/2} \cdot (x(1), x(3), x(5), \dots, x(N-1)) \end{align}\]

  • \(N/2\) 크기의 두 DFT로 부터 \(N\) 크기의 전체 DFT를 다음과 같이 계산할 수 있다. \[ C(k) = \sigma_N^k \cdot B(k)\\ X(k) = A(k) + C(k)\\ X(N/2 + k) = A(k) - C(k) \] for \(k \in [0: N/2 - 1]\)

  • 숫자 \(\sigma_N^k\)는 “twiddle factor”라고도 한다. \(N\)이 2의 거듭제곱인 경우, 이 아이디어는 \(\mathrm{DFT}_{1}\)(\(N=1\)의 경우)의 계산에 도달할 때까지 재귀적으로 적용될 수 있다.

def twiddle(N):
    """Generate the twiddle factors used in the computation of the fast Fourier transform (FFT)
    Args:
        N (int): Number of samples

    Returns:
        sigma (np.ndarray): The twiddle factors
    """
    k = np.arange(N // 2)
    sigma = np.exp(-2j * np.pi * k / N)
    return sigma


def fft(x):
    """Compute the fast Fourier transform (FFT)
    Args:
        x (np.ndarray): Signal to be transformed

    Returns:
        X (np.ndarray): Fourier transform of x
    """
    x = x.astype(np.complex128)
    N = len(x)
    log2N = np.log2(N)
    assert log2N == int(log2N), 'N must be a power of two!'
    X = np.zeros(N, dtype=np.complex128)

    if N == 1:
        return x
    else:
        this_range = np.arange(N)
        A = fft(x[this_range % 2 == 0])
        B = fft(x[this_range % 2 == 1])
        C = twiddle(N) * B
        X[:N//2] = A + C
        X[N//2:] = A - C
        return X
N = 16
n = np.arange(N)
k = 4
x = np.cos(2 * np.pi * (k * n / N) + 2 * (np.random.rand(N) - 0.5)) 
X_via_dft = dft(x)
X_via_fft = fft(x)


plt.figure(figsize=(8, 3))

plt.subplot(1, 2, 1)
plt.title('$x$')
plt.plot(x, marker='.', markersize=12)
plt.xlabel('Time (index $n$)')

plt.subplot(1, 2, 2)
plt.title('$|X|$')
plt.plot(np.abs(X_via_dft), marker='.', markersize=10, label='dft')
plt.plot(np.abs(X_via_fft), linestyle='--', color='pink', marker='.', markersize=6, label='fft')
plt.xlabel('Frequency (index $k$)')
plt.legend()

plt.tight_layout()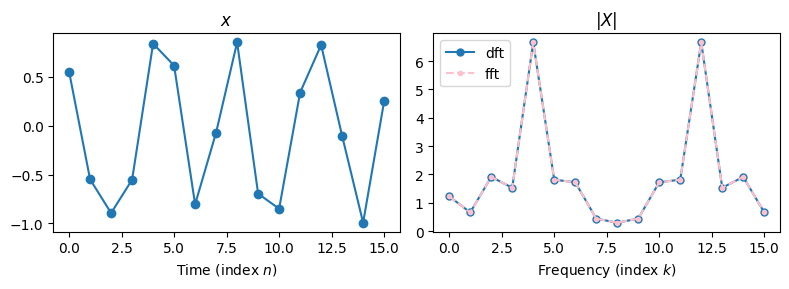

계산 복잡성

  • FFT는 전체 작업 수를 \(N^2\)(일반적인 행렬-벡터 곱 \(\mathrm{DFT}_N \cdot x\)를 계산할 때 필요함)에서 \(N\log_2N\) 정도로 줄인다. 예를 들어 \(N=2^{10}=1024\)를 사용하면 원래의 접근 방식의 \(N^2=1048576\) 작업 대신 FFT에 대략 \(N\log_2N=10240\)가 필요하다.

  • Python 코드의 작은 비트의 시간을 측정하는 간단한 방법을 제공하는 timeit 모듈을 사용하여 실행 시간을 비교한다.

N = 512
n = np.arange(N)
x = np.sin(2 * np.pi * 5 * n / N )

print('Timing for DFT: ', end='')
%timeit dft(x)
print('Timing for FFT: ', end='')
%timeit fft(x)
Timing for DFT: 284 ms ± 6.98 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Timing for FFT: 9.31 ms ± 216 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
import timeit

Ns = [2 ** n for n in range(5, 11)]
times_dft = []
times_fft = []
execuctions = 5

for N in Ns:
    n = np.arange(N)
    x = np.sin(2 * np.pi * 5 * n / N )
    
    time_dft = timeit.timeit(lambda: dft(x), number=execuctions) / execuctions
    time_fft = timeit.timeit(lambda: fft(x), number=execuctions) / execuctions
    times_dft.append(time_dft)
    times_fft.append(time_fft)
    
plt.figure(figsize=(6, 3))
    
plt.plot(Ns, times_dft, '-xk', label='DFT')
plt.plot(Ns, times_fft, '-xr', label='FFT')
plt.xticks(Ns)
plt.legend()
plt.grid()
plt.xlabel('$N$')
plt.ylabel('Runtime (seconds)');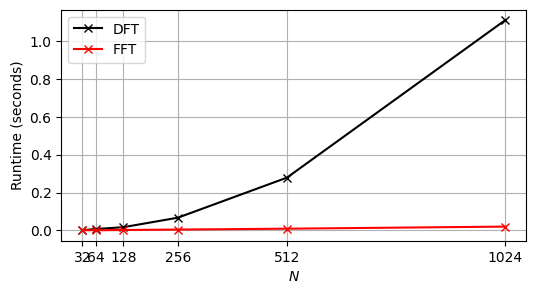

  • FFT의 경우 계산이 훨씬 빠른 것을 볼 수 있다.

FFT 예시

  • librosa
x, sr = librosa.load("../audio/c_strum.wav")
print(x.shape)
print(sr)
ipd.Audio(x, rate=sr)
(102400,)
22050
X = scipy.fft.fft(x)
X_mag = np.absolute(X)
f = np.linspace(0, sr, len(X_mag)) # frequency variable
plt.figure(figsize=(6, 2))
plt.plot(f, X_mag) # magnitude spectrum
plt.xlabel('Frequency (Hz)')
plt.show()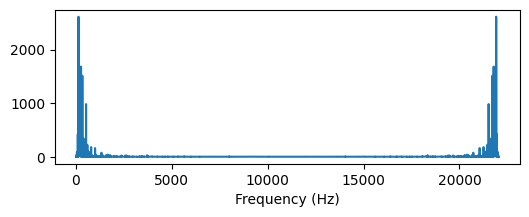

# zoom in
plt.figure(figsize=(6, 2))
plt.plot(f[:5000], X_mag[:5000])
plt.xlabel('Frequency (Hz)')
plt.show()

DFT - 위상(Phase)

  • DFT 계산 결과, 복소 푸리에 계수가 나온다. 이 각 계수는 크기(magnitude) 및 위상(phase) 구성 요소로 나타낼 수 있다.

푸리에 계수의 극좌표 표현 (Polar Representation of Fourier Coefficients)

  • \(x=(x(0), x(1), ..., x(N-1))\)을 샘플 \(x(n)\in\mathbb{R}\) for \(n\in[0:N-1]\)을 가지는 시그널이라고 하자. 복소 푸리에 계수 \(c_k:=X(k)\in\mathbb{C}\) for \(k\in[0:N-1]\)는 DFT에 계산되어 다음과 같다. \[ c_k :=X(k) = \sum_{n=0}^{N-1} x(n) \exp(-2 \pi i k n / N). \]

  • \(c_k = a_k + i b_k\)를 실수부 \(a_k\in\mathbb{R}\)와 허수부 \(b_k\in\mathbb{R}\)로 구성된 복소수라고 할 때,

  • 절대값은 \(|c_k| := \sqrt{a_k^2 + b_k^2}\)이고,

  • 각도(래디안 단위)는 \(\gamma_k := \mathrm{angle}(c_k) := \mathrm{atan2}(b_k, a_k) \in [0,2\pi)\)이다.

  • 지수 함수를 쓰면, 다음의 극좌표 표현을 얻는다. \[ c_k = |c_k| \cdot \mathrm{exp}(i \gamma_k). \]

최적화 Optimality 속성

  • \(\mathbf{cos}_{k,\varphi}:[0:N-1]\to\mathbb{R}\)를 주파수 파라미터 \(k\) 및 위상 \(\varphi\in[0 ,1)\)와 함께 샘플 정현파(sinusoid)라고 하면 다음과 같이 정의된다. \[ \mathbf{cos}_{k,\varphi}(n) = \sqrt{2}\mathrm{cos}\big( 2\pi (kn/N - \varphi) \big) \] for \(n\in[0,N-1]\)

  • 직관적으로 말하자면, 길이 \(N\)의 이산 신호 \(x\)와 주파수 파라미터 \(k\)에 대한 푸리에 변환을 계산할 때 신호 \(x\)와 정현파 \(\mathbf{cos}_{k,\varphi_k}\)의 내적(일종의 상관 관계)을 계산한다.

  • \(\varphi_k\) 위상은 \(\varphi\in[0,1)\)로 \(x\)와 모든 가능한 정현파 \(\mathbf{cos}_{k,\varphi}\) 사이의 상관관계를 최대화한다는 속성을 가지고 있다.

\[ \varphi_k = \mathrm{argmax}_{\varphi\in[0,1)} \langle x | \mathbf{cos}_{k,\varphi} \rangle. \]

  • 복소 푸리에 계수 \(X(k)\)는 기본적으로 복소수의 각도로 주어지는 이 최적 위상을 인코딩한다. 보다 정확하게 \(\gamma_k\)를 \(X(k)\)의 각도라고 하면, 최적 위상 \(\varphi_k\)가 다음과 같이 주어진다는 것을 알 수 있다.

\[ \varphi_k := - \frac{\gamma_k}{2 \pi}. \]

# Generate a chirp-like test signal (details not important)
N = 256
t_index = np.arange(N)
x = 1.8 * np.cos(2 * np.pi * (3 * (t_index * (1 + t_index / (4 * N))) / N))

k = 4
exponential = np.exp(-2 * np.pi * 1j * k * t_index / N)
X_k = np.sum(x * exponential)
phase_k = - np.angle(X_k) / (2 * np.pi)

def compute_plot_correlation(x, N, k, phase):
    sinusoid = np.cos(2 * np.pi * (k * t_index / N - phase)) 
    d_k = np.sum(x * sinusoid)
    plt.figure(figsize=(6,1.5))
    plt.plot(t_index, x, 'k')
    plt.plot(sinusoid, 'r')
    plt.title('Phase = %0.2f; correlation = %0.2f (optimal  = %0.2f)' % (phase, d_k, np.abs(X_k)))
    plt.tight_layout()
    plt.show()

print('Sinusoid with phase from Fourier coefficient resulting in an optimal correlation.')    
compute_plot_correlation(x, N, k, phase=phase_k)

print('Sinusoid with an arbitrary phase resulting in a medium correlation.')  
compute_plot_correlation(x, N, k, phase=0.4)

print('Sinusoid with a phase that yields a correlation close to zero.')  
compute_plot_correlation(x, N, k, phase=0.51)
Sinusoid with phase from Fourier coefficient resulting in an optimal correlation.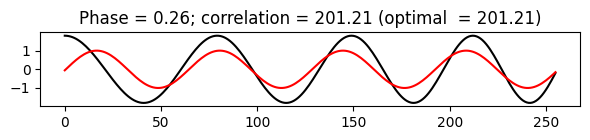

Sinusoid with an arbitrary phase resulting in a medium correlation.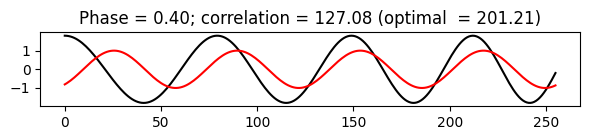

Sinusoid with a phase that yields a correlation close to zero.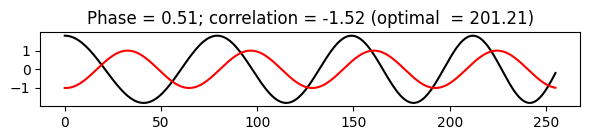

출처:

  • https://www.audiolabs-erlangen.de/resources/MIR/FMP/C2/C2.html

구글 Colab 링크

\(\leftarrow\) 3.1. 복소수와 지수함수
3.3. 단기 푸리에 변환 (STFT) (1) \(\rightarrow\)