from collections import OrderedDict
import numpy as np
import IPython.display as ipd
import pandas as pd6.1. 화성의 기본 이론
Basic Theory of Harmony
화음 인식에 대해 본격적으로 다루기 전에, 화성의 기본 개념을 알아본다. 음정(interval), 화음(chord), 음계(scale) 등에 대해 설명한다.
이 글은 FMP(Fundamentals of Music Processing) Notebooks을 참고로 합니다.
음정(Interval)
음악에서 음정(interval)은 두 피치(pitch) 사이의 차이로 간단하게 정의될 수 있다.
하지만 이 정의는 피치의 기본 개념이 이미 다소 모호하다는 점에서 문제가 있다. 피치는 주파수 관련 로그 스케일에서 소리의 순서를 지정할 수 있는 지각적(perceptual) 속성이다. 악기에서 특정 피치의 음을 연주할 때, 결과적인 음악 톤은 부분음(partial)이라고 하는 특정 주파수가 지배한다.
가장 낮은 부분음의 주파수를 기본 주파수(fundamental freuqency)라고 하며 일반적으로 피치와 관련된 주파수이다. 하모니 소리(harmonic sound)의 경우 부분음은 기본 주파수의 정수 배수인 고조파(harmonics)에 가깝다.
음악에서 가장 기본적인 음정은 옥타브이며, 기본 주파수의 절반 또는 두 배인 피치와 다른 피치 사이의 거리로 정의된다.
이 기본 음정을 시작으로 고조파의 주파수 관계(물리적 접근), 기하학적 관계(수학적 접근) 또는 음의 관계(음악적 접근)를 고려하여 음정의 개념을 정의할 수 있다. 이러한 접근 방식은 음정에 대해 약간 다른 개념들로 이어지지만, 동일한 “음정 이름”으로 여겨진다.
반음 차이 (Semitone Differences)
12 평균율 음계를 가정하면 한 옥타브는 로그 주파수 축에서 등간격으로 배치된 12개의 음계 단계로 세분화 된다.
이 음계에서 가능한 가장 작은 간격을 반음(semitone) 이라고 하며, 이는 두 개의 연이은 음계 단계 간의 차이이다.
주파수 측면에서 반음은 (차이가 아닌) 비율을 나타내며 센트(cents) 라는 로그 단위를 사용하여 지정할 수 있다.
\(\omega_1\)와 \(\omega_2\)라고 하는 두 주파수 간의 센트 차이는 다음과 같다. \[\log_2\left(\frac{\omega_1}{\omega_2}\right)\cdot 1200\]
따라서 평균율 음계에서 반음은 \(100\) 센트에 해당한다.
반음의 개념을 바탕으로 서양 음악 이론에서 사용되는 서로 다른 음정을 지정할 수 있다. 이러한 음정에 대한 명명은 과거의 관행을 기반으로 한다. 특히, “음정 이름”은 낮은 음과 높은 음 사이의 반음 차이를 설명할 뿐만 아니라 악보 표기법에서 음정을 지정하는 방법도 설명할 수 있다.
서로 다른 음표 기호가 동일한 음을 나타낼 수도 있으며, 이는 이명동음적 상등(enharmonic equivalence) 으로 알려져 있다. 유사하게, 반음으로 측정될 때(동일 평균율 음계로 가정) 동일한 거리에 해당하는 음악적으로 다른 음정(다른 음정 이름으로 지칭됨) 사이에는 “enharmonic equivalence”이 존재한다. 예를 들어, “augmented unison”과 “minor second”라는 두 개의 음정은 모두 한 반음의 차이를 표현하지만 악보 표기를 사용할 때는 다르게 지정된다.
여기서는 음정을 지나치게 단순화되더라도 악보를 무시하고 음정 사이의 거리(반음 단위)로 생각하기로 하자.
다음 그림은 가장 일반적인 음정 이름(C4를 낮은 음으로 사용)과 그 의미를 반음 차이(\(\Delta\)로 표시)로 나타낸 것이다.
ipd.Image("../img/6.chord_recognition/FMP_C5_F02b.png", width=600)
주파수 비율(Frequency Ratios)
음정의 개념은 피치의 부분음들 사이에서 자연적으로 발생하는 주파수 관계를 고려하여 물리적인 관점에서 접근할 수 있다. 고조파는 톤의 배음열을 형성하는 기본 주파수의 정수배이다.
물리적 접근에서는 동일한 고조파 계열 내에서 발생하는 부분음 간의 주파수 관계에서 음정을 도출한다. 다음 그림은 음표 C2의 고조파 시리즈를 보여준다.
ipd.Image("../img/6.chord_recognition/FMP_C5_F04.png", width=600)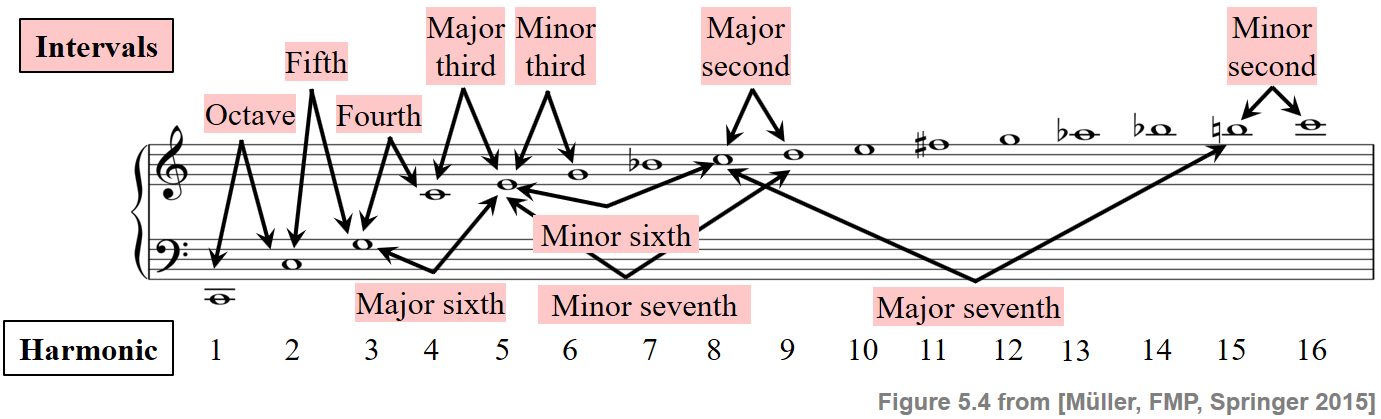
예를 들어, 옥타브(octave)는 처음 두 부분음 사이의 음정(interval)이고, 5도(fifth)는 두 번째와 세 번째 부분음 사이의 음정이고, 4도(fourth)는 세 번째와 네 번째 부분음 사이의 음정으로 발생하는 식으로 이어진다.
이 관찰은 작은 정수의 비율을 기반으로 하는 음정의 정의로 이어진다. 이렇게 정의된 간격을 순수(pure) 또는 단순(just) 음정이라고도 한다. 마찬가지로 고조파에 기반한 음악 조율은 순정률(pure (or just) intonation) 으로 알려져 있다.
순정률 외에도, 주파수 비율 측면에서 음정을 정의하는 데 사용할 수 있는 더 많은 조율 시스템이 있다.
알려진 가장 오래된 튜닝 시스템은 그리스 철학자이자 수학자 피타고라스(기원전 6세기)에 의해 소개되었다. 기하학적 동기가 부여된 피타고라스 튜닝은 옥타브의 주파수 비율 \(1:2\)와 5도의 비율 \(2:3\)에만 기반한다. 다른 모든 음정은 5도와 옥타브를 적절하게 더하거나 빼서 그 비율에서 얻는다. 이로 인해 2의 거듭제곱 또는 3의 거듭제곱만 포함하는 주파수 비율로 표현할 수 있는 음정이 생성된다.
다음 그림에서는 간격의 다양한 정의와 그 관계를 보여준다. 왼쪽 열부터 보면 반음의 차이(\(\Delta\)), 음정의 이름, C4를 근음(root note)으로 가정한 음정, 순정률에 대한 비율(JI), 피타고라스 비율(Pyt)이 나와있다.
ipd.Image("../img/6.chord_recognition/FMP_C5_F03.png", width=400)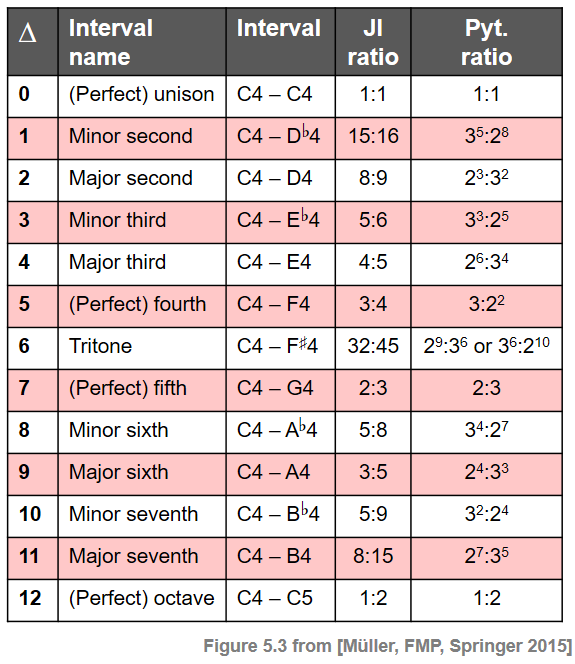
- 다음 코드 셀에서는 평균율(ET), 순음률(JI) 및 피타고라스 튜닝(Pyt)과 관련하여 다양한 음정의 정현파(sinusodial) 음향화(sonification)를 제공한다.
- 또한 ET 기반 및 JI 기반 간격(JI Dev)과 ET 기반 및 Pyt 기반 간격(Pyt Dev) 간의 편차(센트 단위)를 지정한다.
def f_pitch(p):
frequency = 2 ** ((p - 69) / 12) * 440
return frequency
diff_semitones = ['0','1','2','3','4','5','6','7','8','9','10','11','12',]
JI_frac = ['$1:1$', '$15:16$', '$8:9$', '$5:6$', '$4:5$', '$3:4$', '$32:45$',
'$2:3$', '$5:8$', '$3:5$', '$5:9$', '$8:15$', '$1:2$']
JI_ratio = np.asarray([1, 15/16, 8/9, 5/6, 4/5, 3/4, 32/45, 2/3, 5/8, 3/5, 5/9, 8/15, 1/2])
pyt_frac = ['$1:1$', '$3^5:2^8$', '$2^3:3^2$', '$3^3:2^5$', '$2^6:3^4$', '$3:2^2$', '$2^9:3^6$',
'$2:3$', '$3^4:2^7$', '$2^4:3^3$', '$3^2:2^4$', '$2^7:3^5$', '$1:2$']
pyt_ratio = np.asarray([1, 243/256, 8/9, 27/32, 64/81, 3/4, 512/729, 2/3, 81/128, 16/27, 9/16, 128/243, 1/2])
p = 60
omega = f_pitch(p)
freq_JI = omega / JI_ratio
freq_pyt = omega / pyt_ratio
notes = np.asarray(range(p, p + 13))
freq_center = f_pitch(notes)
freq_deviation_cents_JI = np.log2(freq_JI / freq_center) * 1200
freq_deviation_cents_pyt = np.log2(freq_pyt / freq_center) * 1200
duration = 1
Fs = 4000
N = int(duration * Fs)
t = np.arange(0, N) / Fs
def generate_sinusoid(omega, t):
return np.sin(2 * np.pi * omega * t)
def generate_sinusoid_list(freq_list, x_ref=[]):
sinusoid_list = []
for f in freq_list:
s = generate_sinusoid(f, t)
x = np.concatenate((x_ref, s))
sinusoid_list.append(x)
return sinusoid_list
x_ref = generate_sinusoid(omega, t)
sinusoid_center = generate_sinusoid_list(freq_center, x_ref)
sinusoid_JI = generate_sinusoid_list(freq_JI, x_ref)
sinusoid_pyt = generate_sinusoid_list(freq_pyt, x_ref)
# Generation of html table
def generate_audio_tag_html_list(sinusoid_list, Fs):
audio_tag_html_list = []
for i in range(len(sinusoid_list)):
audio_tag = ipd.Audio( sinusoid_list[i], rate=Fs)
audio_tag_html = audio_tag._repr_html_().replace('\n', '').strip()
audio_tag_html = audio_tag_html.replace('<audio ',
'<audio style="width: 110px; height: 30px;"')
audio_tag_html_list.append(audio_tag_html)
return audio_tag_html_list
audio_tag_html_center = generate_audio_tag_html_list(sinusoid_center, Fs=Fs)
audio_tag_html_JI = generate_audio_tag_html_list(sinusoid_JI, Fs=Fs)
audio_tag_html_pyt = generate_audio_tag_html_list(sinusoid_pyt, Fs=Fs)pd.options.display.float_format = '{:,.1f}'.format
pd.set_option('display.max_colwidth', None)
df = pd.DataFrame(OrderedDict([
('$\Delta$', diff_semitones),
('Interval name', ['(Perfect) unison','Minor second','Major second','Minor Third',
'Major Third','(Perfect) fourth', 'Tritone','(Perfect) fifth',
'Minor sixth','Major sixth','Minor seventh','Major seventh','(Perfect) octave']),
(' Interval', ['C4–C4','C4–C$^\sharp$4','C4–D4',
'C4–D$^\sharp$4','C4–E4','C4–F4',
'C4–F$^\sharp$4','C4–G4','C4–G$^\sharp$4',
'C4–A4','C4–A$^\sharp$4', 'C4–B4','C4–C4']),
('ET Sinusoid', audio_tag_html_center),
('   JI Ratio', JI_frac),
('JI Sinusoid', audio_tag_html_JI),
('JI Dev', freq_deviation_cents_JI),
('   Pyt Ratio', pyt_frac),
('Pyt Sinusoid', audio_tag_html_pyt),
('Pyt Dev', freq_deviation_cents_pyt)]))
df.index = np.arange(1, len(df) + 1)
ipd.HTML(df.to_html(escape=False, index=False))| $\Delta$ | Interval name | Interval | ET Sinusoid | JI Ratio | JI Sinusoid | JI Dev | Pyt Ratio | Pyt Sinusoid | Pyt Dev |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (Perfect) unison | C4–C4 | $1:1$ | 0.0 | $1:1$ | 0.0 | |||
| 1 | Minor second | C4–C$^\sharp$4 | $15:16$ | 11.7 | $3^5:2^8$ | -9.8 | |||
| 2 | Major second | C4–D4 | $8:9$ | 3.9 | $2^3:3^2$ | 3.9 | |||
| 3 | Minor Third | C4–D$^\sharp$4 | $5:6$ | 15.6 | $3^3:2^5$ | -5.9 | |||
| 4 | Major Third | C4–E4 | $4:5$ | -13.7 | $2^6:3^4$ | 7.8 | |||
| 5 | (Perfect) fourth | C4–F4 | $3:4$ | -2.0 | $3:2^2$ | -2.0 | |||
| 6 | Tritone | C4–F$^\sharp$4 | $32:45$ | -9.8 | $2^9:3^6$ | 11.7 | |||
| 7 | (Perfect) fifth | C4–G4 | $2:3$ | 2.0 | $2:3$ | 2.0 | |||
| 8 | Minor sixth | C4–G$^\sharp$4 | $5:8$ | 13.7 | $3^4:2^7$ | -7.8 | |||
| 9 | Major sixth | C4–A4 | $3:5$ | -15.6 | $2^4:3^3$ | 5.9 | |||
| 10 | Minor seventh | C4–A$^\sharp$4 | $5:9$ | 17.6 | $3^2:2^4$ | -3.9 | |||
| 11 | Major seventh | C4–B4 | $8:15$ | -11.7 | $2^7:3^5$ | 9.8 | |||
| 12 | (Perfect) octave | C4–C4 | $1:2$ | 0.0 | $1:2$ | 0.0 |
협화음과 불협화음 (Consonance and Dissonance)
조화 부분음(harmonic partials)에 기초한 순정률을 사용하여, \(1:1\)(1도; unison), \(1:2\)(옥타브; octave), \(2:3\)(5도), 또는 \(3:4\)(4도)와 같은 작은 정수 비로 특정 음정이 설명될 수 있음을 보았다.
이러한 음정은 고조파 시리즈의 배음에서 자연스럽게 나타나며 대체로 일관되고 만족스러운(pleasant) 것으로 인식된다.
보다 일반적으로 사용되는 협화음(consonance) 이라는 용어는 동시에 연주될 때 대부분의 사람들에게 듣기 좋게 들리는 음의 조합을 의미한다. 반대로 불협화음(dissonance) 이라는 용어는 거칠거나 불쾌하게 들리는 음의 조합을 가리키는 데 사용된다. 협화음은 불안정한 것으로 간주되는 불협화음(전이 특성을 가짐)과 달리 안정적인 것으로 간주된다.
협화음과 불협화음의 정의는 음악적, 물리적, 지각적 기준에 따라 다양하다.
음정의 경우, 1도, 옥타브, 5도, 4도는 일반적으로 완전(perfect) 협화음으로 간주된다. 따라서 이러한 음정을 완전음정(perfect interval) 이라고도 한다.
장3도(major thirds)와 단3도(minor thirds), 장6도(major sixths)와 단6도(minor sixth)는 여전히 협화음으로 인식되지만 그 정도는 낮다 (불완전 협화음; imperfect consonance).
다른 음정은 일반적으로 불협화음으로 간주된다. 특히 가장 불협화음 음정인 트라이톤 음정(tritone interval) 이 있다. 마지막 절에서 보듯이 순정률에서 트라이톤(tritone)의 주파수 비율은 가장 큰 정수를 포함한다.
음을 동시에 연주할 때 협화음의 정도는 연주한 음의 화성이 일치하는 정도와 관련이 있다. 이러한 관점에서 볼 때, 협화음은 두 음 사이의 음정 크기뿐만 아니라 결과 소리의 결합된 스펙트럼 분포에 따라 달라진다.
다음 코드 예에서 동시 음정(harmonic 음정이라고도 함)은 서로 다른 조음 체계에 따라 정현파로 생성된다.
duration = 3
Fs = 4000
N = int(duration * Fs)
t = np.arange(0, N) / Fs
def generate_sinusoid_interval_list(freq_list, x_ref=[]):
sinusoid_list = []
for f in freq_list:
s = generate_sinusoid(f, t)
x = x_ref + s
sinusoid_list.append(x)
return sinusoid_list
x_ref = generate_sinusoid(omega, t)
sinusoid_center = generate_sinusoid_interval_list(freq_center, x_ref)
sinusoid_JI = generate_sinusoid_interval_list(freq_JI, x_ref)
sinusoid_pyt = generate_sinusoid_interval_list(freq_pyt, x_ref)
sinusoid_sum = list(range(len(freq_center)))
for i in range(len(freq_center)):
sinusoid_sum[i] = (sinusoid_center[i] + sinusoid_JI[i] + sinusoid_pyt[i]) / 3
# Generation of html table
def generate_audio_tag_html_list(sinusoid_freq_list, Fs):
audio_tag_html_list = []
for i in range(len(sinusoid_freq_list)):
audio_tag = ipd.Audio( sinusoid_freq_list[i], rate=Fs)
audio_tag_html = audio_tag._repr_html_().replace('\n', '').strip()
audio_tag_html = audio_tag_html.replace('<audio ',
'<audio style="width: 110px; height: 30px;"')
audio_tag_html_list.append(audio_tag_html)
return audio_tag_html_list
audio_tag_html_center = generate_audio_tag_html_list(sinusoid_center, Fs=Fs)
audio_tag_html_JI = generate_audio_tag_html_list(sinusoid_JI, Fs=Fs)
audio_tag_html_pyt = generate_audio_tag_html_list(sinusoid_pyt, Fs=Fs)
pd.options.display.float_format = '{:,.1f}'.format
pd.set_option('display.max_colwidth', None)
df = pd.DataFrame(OrderedDict([
('Delta', diff_semitones),
('Interval name', ['(Perfect) unison','Minor second','Major second','Minor Third',
'Major Third','(Perfect) fourth', 'Tritone','(Perfect) fifth',
'Minor sixth','Major sixth','Minor seventh','Major seventh','(Perfect) octave']),
(' Interval', ['C4–C4','C4–C$^\sharp$4','C4–D4',
'C4–D$^\sharp$4','C4–E4','C4–F4',
'C4–F$^\sharp$4','C4–G4','C4–G$^\sharp$4',
'C4–A4','C4–A$^\sharp$4', 'C4–B4','C4–C4']),
('ET Sinusoid', audio_tag_html_center),
('   JI Ratio ', JI_frac),
('JI Sinusoid', audio_tag_html_JI),
('JI Dev.', freq_deviation_cents_JI),
('   Pyt Ratio ', pyt_frac),
('Pyt Sinusoid', audio_tag_html_pyt),
('Pyt Dev.', freq_deviation_cents_pyt)]))
df.index = np.arange(1, len(df) + 1)
ipd.HTML(df.to_html(escape=False, justify='center', index=False))| Delta | Interval name | Interval | ET Sinusoid | JI Ratio | JI Sinusoid | JI Dev. | Pyt Ratio | Pyt Sinusoid | Pyt Dev. |
|---|---|---|---|---|---|---|---|---|---|
| 0 | (Perfect) unison | C4–C4 | $1:1$ | 0.0 | $1:1$ | 0.0 | |||
| 1 | Minor second | C4–C$^\sharp$4 | $15:16$ | 11.7 | $3^5:2^8$ | -9.8 | |||
| 2 | Major second | C4–D4 | $8:9$ | 3.9 | $2^3:3^2$ | 3.9 | |||
| 3 | Minor Third | C4–D$^\sharp$4 | $5:6$ | 15.6 | $3^3:2^5$ | -5.9 | |||
| 4 | Major Third | C4–E4 | $4:5$ | -13.7 | $2^6:3^4$ | 7.8 | |||
| 5 | (Perfect) fourth | C4–F4 | $3:4$ | -2.0 | $3:2^2$ | -2.0 | |||
| 6 | Tritone | C4–F$^\sharp$4 | $32:45$ | -9.8 | $2^9:3^6$ | 11.7 | |||
| 7 | (Perfect) fifth | C4–G4 | $2:3$ | 2.0 | $2:3$ | 2.0 | |||
| 8 | Minor sixth | C4–G$^\sharp$4 | $5:8$ | 13.7 | $3^4:2^7$ | -7.8 | |||
| 9 | Major sixth | C4–A4 | $3:5$ | -15.6 | $2^4:3^3$ | 5.9 | |||
| 10 | Minor seventh | C4–A$^\sharp$4 | $5:9$ | 17.6 | $3^2:2^4$ | -3.9 | |||
| 11 | Major seventh | C4–B4 | $8:15$ | -11.7 | $2^7:3^5$ | 9.8 | |||
| 12 | (Perfect) octave | C4–C4 | $1:2$ | 0.0 | $1:2$ | 0.0 |
화음 (Chords)
직관적으로 화음(chord) 은 동시에 소리가 나는 여러 음의 그룹이라고 정의할 수 있다.
대부분의 연구자들은 화음이 적어도 세 개의 음을 포함해야 한다는 데 동의하지만, 또다른 연구자들은 두 음의 조합을 화음으로 간주하기도 한다.
화음에 포함된 개별 음의 수에 따라 dyad(음정에 해당하는 두 개의 음표), triad(세 개의 음표), tetrad(네 개의 음표) 등이 있다.
화성 분석에서 한 옥타브 또는 몇 옥타브 떨어져 있는 음은 종종 동일한 “음질(sound quality)”에 속하는 것으로 간주된다. 따라서 화음의 개념을 정의할 때 별개의 음(note)이라기보다는 별개의 피치 클래스(pitch class)로 말하는 것이 더 정확할 수 있다.
3화음 (Triads)
다음과 같은 소수의 화음으로 제한하여 살펴보자.
서양 음악에서 가장 중요한 3화음은 3도(thirds)로 쌓일 수 있는 3개의 음으로 구성된다. 3도를 쌓을 때 가장 낮은 음을 근음(root note) 이라고 한다.
단3도(반음 3개)와 장3도(반음 4개)가 있으므로, 다음의 4개의 3화음을 구분할 수 있다: 장3화음(major triad), 단3화음(minor triad), 감3화음(diminished triad), 증3화음(augmented triad).
다음 그림은 근음 C4에 대한 이러한 유형의 3화음을 보여준다.
ipd.Image("../img/6.chord_recognition/FMP_C5_F05_triad.png",width=600)
각 화음 유형은 서로 다른 근음에 따라 연주될 수 있다.
주어진 근음에 관계없이 4개의 3화음 형식은 청취자가 인식하는 방식에 따라 질이 다르다.
장3도와 완전5도로 구성된 장(major)3화음은 협화음정을 구성한다. 또한 세 구성음의 부분음 사이에 일치도가 높다. 그 결과 장3화음의 소리는 종종 일관되고 유쾌하며 행복한 것으로 묘사된다.
두 번째 음의 피치를 반음 낮추면 장3화음이 단(minor)3화음으로 바뀐다. 여전히 협화음이 있고 일관성 있는 것으로 간주되지만 단화음은 종종 슬프고 우울하거나 침울한 것으로 인식된다.
감(diminished)3화음 및 증(augmented)3화음의 경우 구성음의 부분음이 거의 겹치지 않으며 이러한 3화음은 일반적으로 불협화음 및 불안정한 것으로 인식된다. 종종 감 및 증3화음은 장화음과 단화음을 기반으로 보다 안정적인 화성 사이를 이동하기 위해 전환 악절에서 사용된다.
다음은 피아노로 연주되는 \(\mathrm{C}\)-major 및 \(\mathrm{C}\)-minor 화음의 사운드 예이다.
정현파를 사용하여 네 가지 화음 유형 각각의 합성(sythetic) 변형을 생성하자.
print("Major triad")
ipd.display(ipd.Audio(filename="../data_FMP/FMP_C5_F05a_C-Major-Triad_AudioLabs.mp3"))
print("Minor triad")
ipd.display(ipd.Audio(filename="../data_FMP/FMP_C5_F05b_C-Minor-Triad_AudioLabs.mp3"))Major triadMinor triaddef generate_sinusoid_chord(pitches=[69], duration=1, Fs=4000, amplitude_max=0.5):
"""Generate synthetic sound of chord using sinusoids
Args:
pitches (list): List of pitches (MIDI note numbers) (Default value = [69])
duration (float): Duration (seconds) (Default value = 1)
Fs (scalar): Sampling rate (Default value = 4000)
amplitude_max (float): Amplitude (Default value = 0.5)
Returns:
x (np.ndarray): Synthesized signal
"""
N = int(duration * Fs)
t = np.arange(0, N) / Fs
x = np.zeros(N)
for p in pitches:
omega = 2 ** ((p - 69) / 12) * 440
x = x + np.sin(2 * np.pi * omega * t)
x = amplitude_max * x / np.max(x)
return xduration = 2
Fs = 4000
pitches = [60, 64, 67]
x = generate_sinusoid_chord(pitches=pitches, duration=duration, Fs=Fs)
print('Major chord', flush=True)
ipd.display(ipd.Audio(data=x, rate=Fs))
pitches = [60, 63, 67]
x = generate_sinusoid_chord(pitches=pitches, duration=duration, Fs=Fs)
print('Minor chord', flush=True)
ipd.display(ipd.Audio(data=x, rate=Fs))
pitches = [60, 63, 66]
x = generate_sinusoid_chord(pitches=pitches, duration=duration, Fs=Fs)
print('Diminished chord', flush=True)
ipd.display(ipd.Audio(data=x, rate=Fs))
pitches = [60, 64, 68]
x = generate_sinusoid_chord(pitches=pitches, duration=duration, Fs=Fs)
print('Augmented chord', flush=True)
ipd.display(ipd.Audio(data=x, rate=Fs))Major chordMinor chordDiminished chordAugmented chord장화음, 단화음 (Major and Minor Chords)
12개의 서로 다른 근음이 있기 때문에 기본적으로 12개의 장3화음과 12개의 단3화음을 형성할 수 있다.
다음은 각 화음의 가장 낮은 음이 근음인 3화음의 악보 표현을 보여준다. 또한 피아노 녹음과 각 3화음의 합성 버전을 들어보자.
ipd.display(ipd.Image('../img/6.chord_recognition/FMP_C5_F06_major.png'))
ipd.display(ipd.Audio('../data_FMP/FMP_C5_F06_Major-Triads_AudioLabs_NoPedal.mp3'))
ipd.display(ipd.Image('../img/6.chord_recognition/FMP_C5_F06_minor.png'))
ipd.display(ipd.Audio('../data_FMP/FMP_C5_F06_Minor-Triads_AudioLabs_NoPedal.mp3'))
duration = 1
Fs = 4000
x_major = []
pitches = np.array([60, 64, 67])
for i in range(12):
x = generate_sinusoid_chord(pitches=pitches+i, duration=duration, Fs=Fs)
x_major = np.append(x_major, x)
x_minor = []
pitches = np.array([60, 63, 67])
for i in range(12):
x = generate_sinusoid_chord(pitches=pitches+i, duration=duration, Fs=Fs)
x_minor = np.append(x_minor, x)
print('Major chords', flush=True)
ipd.display(ipd.Audio(data=x_major, rate=Fs))
print('Minor chords', flush=True)
ipd.display(ipd.Audio(data=x_minor, rate=Fs))Major chordsMinor chords음 수준에서는 일반적으로 주어진 화음를 실현하기 위한 많은 대안이 있다.
화음의 가장 낮은 음(베이스 음)이 근음일 때 화음는 근음 위치(root position) 또는 정상 형식(normal form) 에 있다고 한다. 근음이 화음에서 연주되는 가장 낮은 음이 아닌 경우 반전(inverted) 이라고 한다.
다음 그림은 정규 형식, 첫 번째 반전(inversion), 두 번째 반전, 옥타브 더블링(doubling)이 있는 화음 및 깨진 화음 (broken chord) (코드의 음을 차례로 연주할 수 있음)을 보여준다.
ipd.display(ipd.Image("../img/6.chord_recognition/FMP_C5_F07.png", width="400"))
ipd.display(ipd.Audio("../data_FMP/FMP_C5_F07_C-Major-Variants_AudioLabs_NoPedal.mp3"))
Fs = 4000
duration = 2
x = []
x = generate_sinusoid_chord(pitches=[60, 64, 67], duration=duration, Fs=Fs)
x = np.append(x,generate_sinusoid_chord(pitches=[64, 67, 72], duration=duration, Fs=Fs))
x = np.append(x,generate_sinusoid_chord(pitches=[67, 72, 76], duration=duration, Fs=Fs))
x = np.append(x,generate_sinusoid_chord(pitches=[60, 64, 67, 72, 76], duration=duration, Fs=Fs))
duration = duration / 8
broken_chord = [60, 64, 67, 72, 76, 67, 72, 76]
for p in broken_chord:
x = np.append(x,generate_sinusoid_chord(pitches=[p], duration=duration, Fs=Fs))
ipd.display(ipd.Audio(data=x, rate=Fs))- 장(major) 화음은 일반적으로 근음의 피치 클래스에 사용되는 것과 동일한 기호로 표시된다.
- 다음부터는 굵은 글씨를 사용하여 화음의 개념과 피치 클래스 또는 음의 개념을 구분한다.
- 단(minor) 화음의 경우 “minor”를 나타내는 \(\mathbf{m}\) 문자를 추가하는 것을 제외하고는 메이저 화음과 동일한 표기법을 사용하는 경우가 많다.
- 예를 들어, \(\mathbf{C}\)로 표시되는 \(\mathrm{C}\)-major 화음은 피치 클래스 \(\mathrm{C}\), \(\mathrm{E}\) 및 \(\mathrm{G}\)가 있는 세 개의 음으로 구성된다. 반면, \(\mathbf{Cm}\)로 표시되는 \(\mathrm{C}\)-minor 화음은 \(\mathrm{C}\), \(\mathrm{E}^\flat\) 및 \(\mathrm{G}\)로 구성된다.
수학적 모형
- 구성 음의 피치 클래스 또는 크로마 값에 의해 장 또는 단 화음이 결정되는 다소 단순한 관점을 채택하면, 각 3화음을 12개의 크로마 속성으로 구성된 \(\{\mathrm{C},\mathrm{C}^\sharp,\mathrm{D},\ldots\mathrm{B}\}\)로 생각할 수 있다.
- 동등하게, 3개 원소의 하위 집합은 하위 집합에 의해 인코딩된 크로마 위치에서 \(1\) 값의 3개 항목이 있는 이진 크로마 벡터로 간주될 수 있다.
- 이 수학적 모형에 기초하여 장3화음 \(\mathbf{C}\)를 12가지 다른 방식으로 순환 이동함으로써 12개의 장화음을 얻을 수 있다. 마찬가지로 \(\mathbf{Cm}\)에서 12개의 단화음을 얻는다.
- 각 \(24\)개의 장 및 단 3화음은 서로 다른 3개 요소 하위 집합으로 이어진다. 즉, 피치 클래스 수준에서 장화음과 단화음은 고유하게 정의된다.
- \(24\)개의 장, 단화음의 크로마 패턴 결과는 다음 그림과 같다.
ipd.Image("../img/6.chord_recognition/FMP_C5_F06.png", width=800)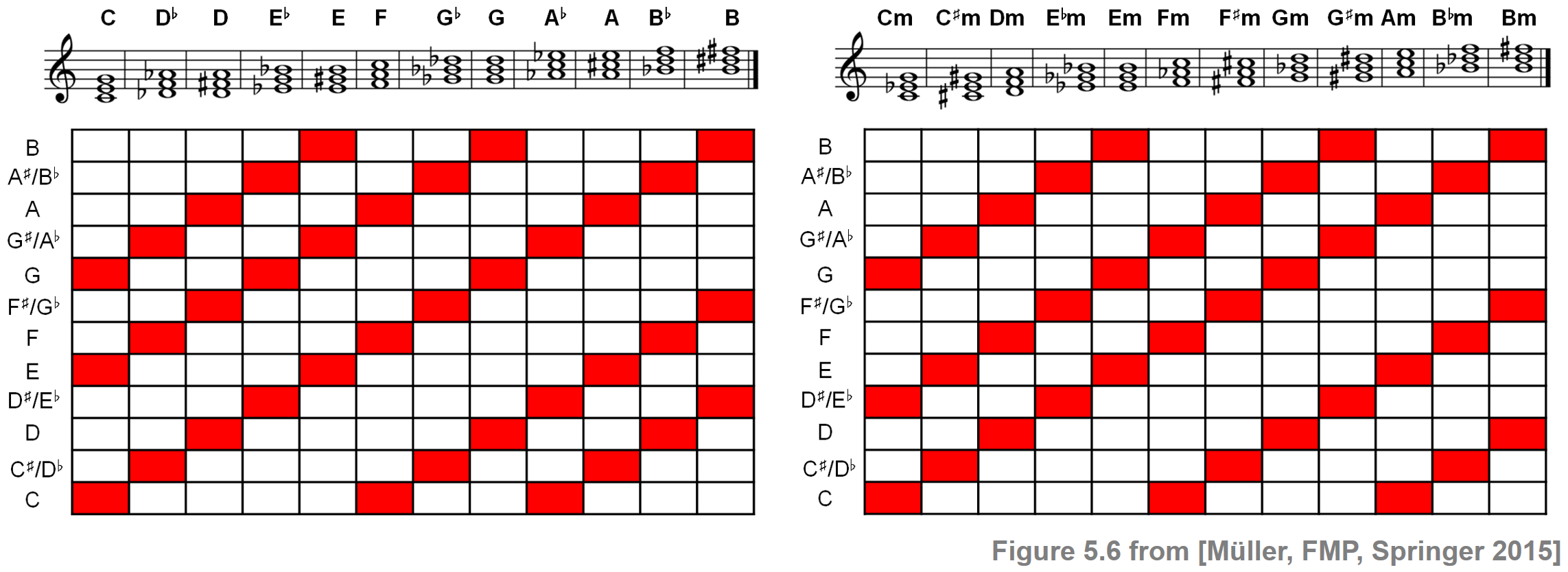
7도화음 등 (Seventh Chords and Beyond)
- 3화음은 4개, 5개 또는 그 이상의 음으로 구성된 보다 복잡한 화음의 하위 집합으로도 나타난다.
- 3화음에 3도 음정을 더 쌓으면 7도 화음이 된다.
- 7화음에는 여러 종류가 있다.
- 장7도 화음은 장3화음 위에 장3도를 쌓아 만든 것으로 주로 팝, 재즈 음악에 사용된다.
- dominant 7도 화음 (장3화음 + 단3도)는 다음 화음으로 리졸브(resolve)되는 경향이 강하다.
- 단7도 화음 (단3화음 + 단3도)은 더 안정적이며 팝/록/재즈와 클래식 음악 모두에 나타난다.
- 반-감(half-diminished)7도 화음 (감3화음 + 장3도)은 낭만주의 음악(예: Richard Wagner)과 재즈 음악에서 광범위하게 사용된다.
- 감7화음 (감3화음 + 단3도)은 3개의 연결된 단3도음으로 구성되어 바로크 음악에서 다른 키로 변조하는 데 사용되었다.
ipd.display(ipd.Image("../img/6.chord_recognition/FMP_C5_SeventhChords.png", width=800))
ipd.display(ipd.Audio("../data_FMP/FMP_C5_F07_Seventh-Chords_AudioLabs_NoPedal.mp3"))
음계와 오도권 (Musical Scales and Circle of Fifths)
음정과 화음 외에도 음계(scale)라고 하는 또 다른 중요한 음악 구조를 설명한다.
다소 단순한 관점으로, 음계는 요소가 일반적으로 오름차순 피치로 정렬되는 일련의 음으로 간주될 수 있다.
화음은 수직 구조로 생각할 수 있지만 음계는 일반적으로 수평 구조와 관련이 있다.
옥타브 등가의 원리를 가정하면, 음계는 일반적으로 단일 옥타브에 걸쳐 있으며 더 높거나 낮은 옥타브의 단순한 패턴 반복이다.
이와 같이 음계는 옥타브 공간을 일정한 수의 음계 단계(scale step)로 나눈 것으로 간주할 수 있다. 여기서 각 음계 단계는 연속되는 두 음 사이의 음정이다.
크로마틱 스케일 / 반음계 (Chromatic Scale)
- 첫 번째 예로, 한 옥타브가 12개의 음계 단계로 세분되는 12음 평균율 음계를 고려해보자. 이 음계는 반음계(chromatic scale)라고도 한다.
- 이 경우 모든 음계 단계는 1반음(또는 \(100\) cents) 크기의 동일한 음정에 해당하며, 다음 그림과 같다(enharmonic equivalence로 두 가지 방법으로 표시). 또한 피아노 녹음과 반음계의 합성 버전(다음 코드 셀)을 들어보자.
ipd.display(ipd.Image("../img/6.chord_recognition/FMP_C5_F08.png", width=500))
ipd.display(ipd.Audio("../data_FMP/FMP_C5_F08_Chromatic-Scale_AudioLabs.mp3"))
def generate_sinusoid_scale(pitches=[69], duration=0.5, Fs=4000, amplitude_max=0.5):
"""Generate synthetic sound of scale using sinusoids
Args:
pitches (list): List of pitchs (MIDI note numbers) (Default value = [69])
duration (float): Duration (seconds) (Default value = 0.5)
Fs (scalar): Sampling rate (Default value = 4000)
amplitude_max (float): Amplitude (Default value = 0.5)
Returns:
x (np.ndarray): Synthesized signal
"""
N = int(duration * Fs)
t = np.arange(0, N) / Fs
x = []
for p in pitches:
omega = 2 ** ((p - 69) / 12) * 440
x = np.append(x, np.sin(2 * np.pi * omega * t))
x = amplitude_max * x / np.max(x)
return xduration = 0.2
Fs = 4000
pitches = [60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72]
x = generate_sinusoid_scale(pitches=pitches, duration=duration, Fs=Fs)
print('Chromatic scale', flush=True)
ipd.display(ipd.Audio(data=x, rate=Fs))Chromatic scale장음계, 단음계 (Major and Minor Scale)
다음에서는 음계 단계를 반음 단위로 지정할 수 있는 반음계의 하위 집합인 음계만 고려한다. 음계에서 단초(1반음)는 half step, 장초(2반음)는 whole step이라고도 한다.
화음과 마찬가지로 서양 음악 이론에서 특히 중요한 두 가지 음계 유형이 있다.
첫 번째 음계 유형은 장음계로 알려져 있으며 7개의 음과 반복되는 옥타브로 구성된다. 장음계의 첫 번째 음은 해당 스케일의 으뜸음 (key note) 라고 한다. 으뜸음에서 시작해 장음계의 이어지는 음 간의 음정의 시퀀스는 다음과 같다(C4를 으뜸음으로 사용).
ipd.display(ipd.Image("../img/6.chord_recognition/FMP_C5_F09a.png", width=500))
ipd.display(ipd.Audio("../data_FMP/FMP_C5_F09a_C-Major-Scale_AudioLabs.mp3"))
- 으뜸음의 크로마 이름은 음계의 이름도 결정한다. 예를 들어, \(\mathrm{C}\)로 시작하는 장음계를 \(\mathrm{C}\)-major scale이라고 한다. 때로는 굵은 글씨의 \(\mathbf{C}\)도 음계를 나타내는 약어로 사용된다.
- \(\mathrm{C}\)-major scale을 순환 이동하여 다른 장음계를 얻을 수 있다.
- 장음계의 음에는 으뜸음에 상대적인 위치를 지정하기 위해 음계도(scale degrees)라고도 하는 이름이 지정된다.
- 으뜸음는 “tonic” 이라고도 하며 음계의 메인 음이다. 음계의 네 번째 음은 “subdominant” 라고 하고 다섯 번째 음은 “dominant” 라고 한다. 나머지 이름은 다음 그림에 나와있다.
ipd.display(ipd.Image("../img/6.chord_recognition/FMP_C5_F09b.png", width=500))
- 두 번째 음계 유형은 단음계이다. 장음계와 유사하게 단음계는 7개의 음과 반복되는 옥타브로 구성된다. 그러나 이번에는 음 사이의 음정 순서는 다음과 같다(C4를 으뜸음으로 사용).
ipd.display(ipd.Image("../img/6.chord_recognition/FMP_C5_F09b.png", width=500))
ipd.display(ipd.Audio("../data_FMP/FMP_C5_F09c_C-Minor-Scale_AudioLabs.mp3"))
- 단음계와 유사한 명명 규칙을 가진 12개의 단음계가 있다. 장음계와 단음계 모두 온음계(diatonic scale) 라는 일반 용어에 포함될 수 있다. 이것은 (정의상) 각 옥타브에 대해 5개의 whole-step과 2개의 half-step이 있는 7음 음계이며, 여기서 두 개의 half-step은 두 개 또는 세 개의 whole-step으로 각각 분리된다.
duration = 0.5
x_maj = generate_sinusoid_scale(pitches=[60, 62, 64, 65, 67, 69, 71, 72], duration=duration, Fs=Fs)
x_min = generate_sinusoid_scale(pitches=[60, 62, 63, 65, 67, 68, 70, 72], duration=duration, Fs=Fs)
print('C-major scale', flush=True)
ipd.display(ipd.Audio(data=x_maj, rate=Fs))
print('C-minor scale (natural)', flush=True)
ipd.display(ipd.Audio(data=x_min, rate=Fs))C-major scaleC-minor scale (natural)기타 음계 (Further Scales)
- 위에서 소개한 단음계(natural minor scale이라고도 함) 외에도 harmonic minor 및 melodic minor scale라는 다른 종류의 단음계들이 있다.
- harmonic minor scale의 음은 natural minor scale와 같지만 7도를 반음 올려 6도와 7도 사이에서 2도가 증가한다.
- 또한 5음으로 구성된 펜타토닉 음계(pentatonic scale), 6음으로 구성된 온음 음계(whole tone scale), 8음으로 구성된 옥타토닉 음계(octatonic scale)(감음 음계) 등이 있다.
print('Harmonic minor scale (7 pitches + octave)', flush=True)
ipd.display(ipd.Image("../img/6.chord_recognition/FMP_C5_FurtherScales_HarmonicMinor.png", width=400))
ipd.display(ipd.Audio("../data_FMP/FMP_C5S1_Scale-Harmonic-Minor_AudioLabs.mp3"))
print('Pentatonic scale (5 pitches + octave)', flush=True)
ipd.display(ipd.Image("../img/6.chord_recognition/FMP_C5_FurtherScales_Pentatonic.png", width=400))
ipd.display(ipd.Audio("../data_FMP/FMP_C5S1_Scale-Pentatonic_AudioLabs.mp3"))
print('Whole tone scale (6 pitches + octave)', flush=True)
ipd.display(ipd.Image("../img/6.chord_recognition/FMP_C5_FurtherScales_WholeTone.png", width=400))
ipd.display(ipd.Audio("../data_FMP/FMP_C5S1_Scale-Whole-Tone_AudioLabs.mp3"))
print('Octatonic scale (8 pitches + octave)', flush=True)
ipd.display(ipd.Image("../img/6.chord_recognition/FMP_C5_FurtherScales_Octatonic.png", width=400))
ipd.display(ipd.Audio("../data_FMP/FMP_C5S1_Scale-Octatonic_AudioLabs.mp3"))Harmonic minor scale (7 pitches + octave)
Pentatonic scale (5 pitches + octave)
Whole tone scale (6 pitches + octave)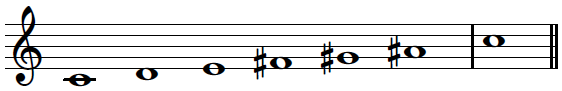
Octatonic scale (8 pitches + octave)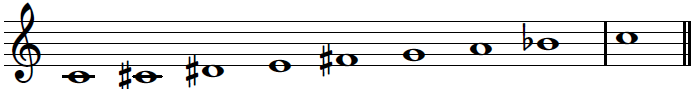
duration = 0.5
x_mh = generate_sinusoid_scale(pitches=[60, 62, 63, 65, 67, 68, 71, 72], duration=duration, Fs=Fs)
x_p = generate_sinusoid_scale(pitches=[60, 62, 64, 67, 69, 72], duration=duration, Fs=Fs)
x_w = generate_sinusoid_scale(pitches=[60, 62, 64, 66, 68, 70, 72], duration=duration, Fs=Fs)
x_o = generate_sinusoid_scale(pitches=[60, 61, 63, 64, 66, 67, 69, 70, 72], duration=duration, Fs=Fs)
print('Harmonic minor scale (7 pitches + octave)', flush=True)
ipd.display(ipd.Audio(data=x_mh, rate=Fs))
print('Pentatonic scale (5 pitches + octave)', flush=True)
ipd.display(ipd.Audio(data=x_p, rate=Fs))
print('Whole tone scale (6 pitches + octave)', flush=True)
ipd.display(ipd.Audio(data=x_w, rate=Fs))
print('Octatonic scale (8 pitches + octave)', flush=True)
ipd.display(ipd.Audio(data=x_o, rate=Fs))Harmonic minor scale (7 pitches + octave)Pentatonic scale (5 pitches + octave)Whole tone scale (6 pitches + octave)Octatonic scale (8 pitches + octave)오도권 (Circle of Fifths)
온음계(diatonic scales)의 특징 중 하나는 6개의 연속적인 완전5도 음정의 체인으로부터 얻을 수 있다는 것이다.
예를 들어, \(\mathrm{C}\)-major 음계는 \(\mathrm{F}\)로 시작하는 6개의 완전5도의 오름차순 체인에서 얻는다.
\[\mathrm{F}-\mathrm{C}-\mathrm{G}-\mathrm{D}-\mathrm{A}-\mathrm{E}-\mathrm{B}\]
ipd.Audio("../data_FMP/FMP_C5S1_Scale-Diatonic-Fifths.mp3")옥타브가 아닌 가장 협화음인 5도 음정은 음, 화음, 음계를 연결할 때 특히 중요한 역할을 한다. 5도와 관련된 모든 음은 온음계에 어느 정도 일관성과 균형을 부여하며 전체 음계를 연관시키는 것도 가능하게 한다.
반음계의 12개 음과 관련 장음계와 단음계 사이의 관계를 시각적으로 표현한 유명한 5도권(circle of fifths)이 있다. 직관적으로 5도권은 서로 다른 음계 사이의 “음악적” 유사성의 정도를 반영한다. 두 음계가 원에 가까울수록 음조(tonal) 측면에서 더 많이 공유한다.
ipd.Image("../img/6.chord_recognition/FMP_C5_F10.png", width=400)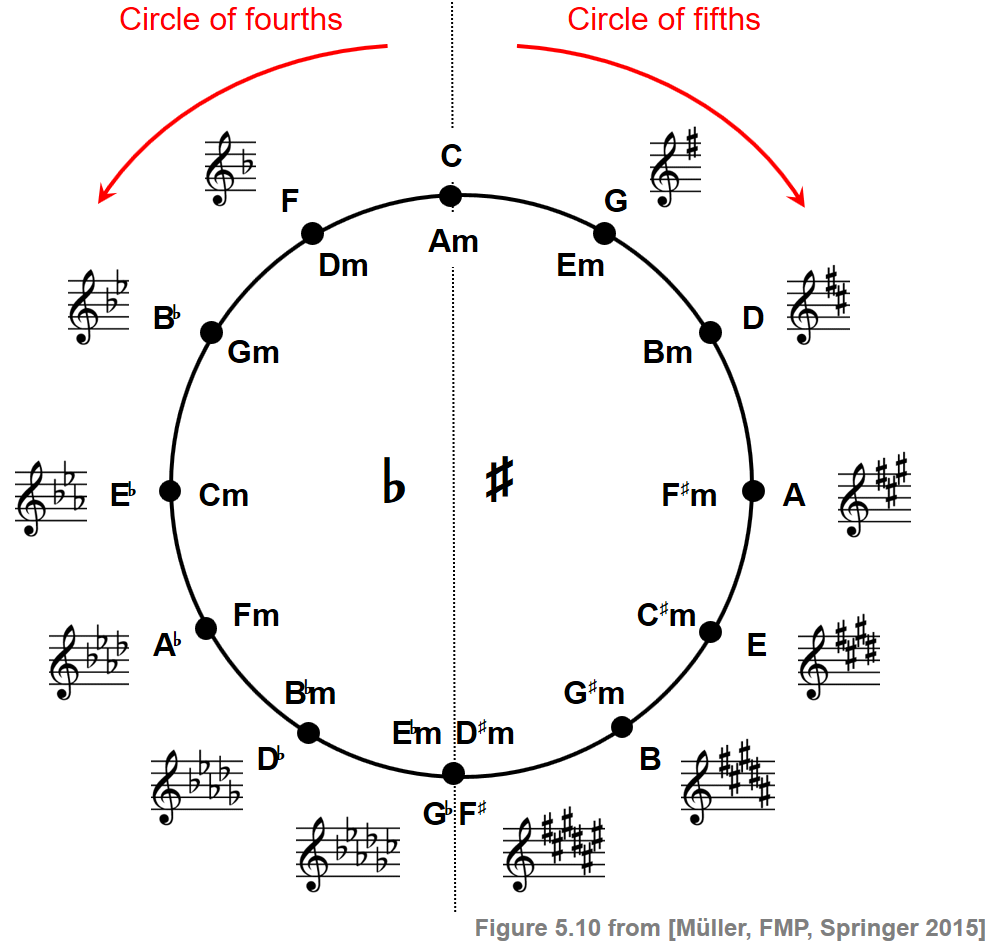
다음 녹음에서 각 음계의 으뜸음(key note)은 시계 방향으로 5도의 원을 그리며 연주된다.
\[\mathrm{C}-\mathrm{G}-\mathrm{D}-\mathrm{A}-\mathrm{E}-\mathrm{B}-\mathrm{G}^\flat-\mathrm{D}^\flat-\mathrm{A}^\flat-\mathrm{E}^\flat-\mathrm{B}^\flat-\mathrm{F}\]
ipd.Audio("../data_FMP/FMP_C5_F10_Circle-Fifths.mp3")음조 (Musical Keys)
좀 더 공식적으로 5도권은 음조(key) 간의 관계를 나타낸다. 이 개념은 장음계와 단음계와 밀접하게 연결되어 있다.
음계는 일반적으로 음조에 사용되는 정렬된 음의 집합이지만 음조는 특정 코드 진행에 의해 설정된 중심이다.
5도권의 상단에는 \(\mathrm{C}\)-major key(C장조)가 있다. 피아노 건반의 흰색 건반에 해당하는 해당 \(\mathrm{C}\)-major scale의 음은 서양 음악 표기법에서 임시표(accidental)(\(\sharp\), \(\flat\))가 필요하지 않다. 결과적으로 \(\mathrm{C}\) major의 조표에는 플랫이나 샤프가 없다.
\(\mathrm{A}\)단조는 해당 음계가 동일한 7개의 음으로 구성되며, \(\mathrm{C}\)-major와 동일한 음조 시그니쳐를 공유한다.
일반적으로 각 장조에는 해당 음계가 동일한 음을 공유하는 단조가 있다. 이 관계를 상대관계(relative relationship) 라고 한다. 위에 표시된 5도권에서 장조는 원 외부에 표시되고 해당 상대적 단조는 원 안에 표시된다.
원의 상단에 있는 \(\mathrm{C}\)장조부터 시작하여 시계 방향으로 오름차순 5도까지 다른 음조를 얻는다.
다음 음조는 \(\mathrm{G}\)장조이며 해당 음계는 \(\mathrm{C}\)-major 스케일과 6개의 음을 공유한다. \(\mathrm{C}\)-major의 \(\mathrm{F}\)만 \(\mathrm{G}\)-major의 \(\mathrm{F}^\sharp\)가 된다. 즉 \(\mathrm{G}\)장조의 조표에 샤프를 도입한다.
동일한 종류의 관계가 5도권을 따라 두 개의 후속 음조 또는 음계 사이에 유지된다. 5도를 위로 진행하면 음계의 1음이 변경되고 조표에 1개의 샤프가 추가된다. 이 과정을 평균율에서 12번 반복하는 경우, 원래의 \(\mathrm{C}\)-major로 돌아가서 원을 닫게 된다.
마찬가지로 오름차순 4도에 해당하는 내림차순 5도로 시계 반대 방향으로 원을 따라 이동할 수 있다. 4도권으로 진행하면 결과 조표에 플랫이 추가된다.
5도권을 따라 정렬된 모든 \(24\) 장단음계의 합성 버전을 들어보자.
duration = 0.25
scale_major = np.array([60, 62, 64, 65, 67, 69, 71, 72])
scale_minor = np.array([57, 59, 60, 62, 64, 65, 67, 69])
scale_major_name = ['C','G','D','A','E','B','F$^\sharp$',
'D$^\\flat$','A$^\\flat$','E$^\\flat$','B$^\\flat$','F','C',]
scale_minor_name = ['Am','Em','Bm','F$^\sharp$m','C$^\sharp$m','G$^\sharp$m','D$^\sharp$m',
'B$^\\flat$m','Fm','Cm','Gm','Dm','Am',]
scale_major_list = []
for i in range(13):
x = generate_sinusoid_scale(pitches=scale_major, duration=duration, Fs=Fs)
scale_major_list.append(x)
scale_major += 7
if scale_major[-1] > 80:
scale_major -= 12
scale_minor_list = []
for i in range(13):
x = generate_sinusoid_scale(pitches=scale_minor, duration=duration, Fs=Fs)
scale_minor_list.append(x)
scale_minor += 7
if scale_minor[-1] > 80:
scale_minor -= 12
audio_tag_html_list_major = []
for i in range(13):
audio_tag = ipd.Audio(scale_major_list[i], rate=Fs)
audio_tag_html = audio_tag._repr_html_().replace('\n', '').strip()
audio_tag_html = audio_tag_html.replace('<audio ',
'<audio style="width: 200px; height: 30px;"')
audio_tag_html_list_major.append(audio_tag_html)
audio_tag_html_list_minor = []
for i in range(13):
audio_tag = ipd.Audio(scale_minor_list[i], rate=Fs)
audio_tag_html = audio_tag._repr_html_().replace('\n', '').strip()
audio_tag_html = audio_tag_html.replace('<audio ',
'<audio style="width: 200px; height: 30px;"')
audio_tag_html_list_minor.append(audio_tag_html)
pd.options.display.float_format = '{:,.1f}'.format
pd.set_option('display.max_colwidth', None)
df = pd.DataFrame(OrderedDict([
('Major', scale_major_name),
(' ', audio_tag_html_list_major),
('Minor', scale_minor_name),
(' ', audio_tag_html_list_minor)]))
#df.index = np.arange(0, len(df))
#df = df.T
ipd.HTML(df.to_html(escape=False, justify='center', index=True, header=True))| Major | Minor | |||
|---|---|---|---|---|
| 0 | C | Am | ||
| 1 | G | Em | ||
| 2 | D | Bm | ||
| 3 | A | F$^\sharp$m | ||
| 4 | E | C$^\sharp$m | ||
| 5 | B | G$^\sharp$m | ||
| 6 | F$^\sharp$ | D$^\sharp$m | ||
| 7 | D$^\flat$ | B$^\flat$m | ||
| 8 | A$^\flat$ | Fm | ||
| 9 | E$^\flat$ | Cm | ||
| 10 | B$^\flat$ | Gm | ||
| 11 | F | Dm | ||
| 12 | C | Am |
출처:
- https://www.audiolabs-erlangen.de/resources/MIR/FMP/C5/C5S1_Intervals.html
- https://www.audiolabs-erlangen.de/resources/MIR/FMP/C5/C5S1_Chords.html
- https://www.audiolabs-erlangen.de/resources/MIR/FMP/C5/C5S1_Scales_CircleFifth.html
\(\leftarrow\) 5.5. 음악 처리의 평가 방법