import os, sys
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from collections import OrderedDict
from scipy import signal
import librosa.display
import IPython.display as ipd
from IPython.display import Image, Audio
path_img = '../img/9.musically_informed_audio_decomposition/'
path_data = '../data_FMP/'
from utils.plot_tools import *
from utils.tempo_tools import compute_novelty_energy9.1. 화성-타악 분리 (HPS)
Harmonic-Percussive Separation
오디오의 하모니(Harmonic) 부분과 타악기(Percussive) 부분을 분리하는 HPS와 HRPS, 그리고 신호의 재구성 방법을 설명한다.
이 글은 FMP(Fundamentals of Music Processing) Notebooks을 참고로 합니다.
Harmonic–Percussive Separation (HPS)
화성음과 타악기 소리
- 음악 사운드는 음향 품질이 다른 광범위한 소리 구성 요소로 구성될 수 있다. 특히 화성음(harmonic)과 타악기(percussive)의 두 가지 넓은 범주의 소리를 고려한다.
- 화성음(harmonic sound)는 피치 사운드로 인식하는 것으로, 멜로디와 화음(chord)을 듣게 만드는 것이다. 화성음의 원형은 스펙트로그램 표현의 가로선에 해당하는 정현파(sinusoid)의 음향적 실현이다. 바이올린 소리는 우리가 화음이라고 생각하는 또 다른 전형적인 예이다. 다시 말하지만, 스펙트로그램에서 관찰된 대부분의 구조는 수평적 특성을 가진다(비록 잡음과 같은 구성 요소와 혼합되어 있음에도 불구하고).
- 반면에 타악기 소리(percussive sound)는 우리가 충돌, 노크, 박수 또는 클릭 등으로 인식하는 것이다. 드럼 스트로크 사운드 또는 음악 톤의 어택 단계에서 발생하는 트랜지언트가 더 일반적인 예이다. 충격음의 원형은 스펙트로그램 표현의 수직선에 해당하는 임펄스(impulse)의 음향적 구현이다.
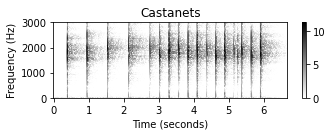
- 다음 예에서는 바이올린 녹음, 캐스터네츠 녹음 및 이 두 녹음의 중첩에 대한 스펙트로그램 표현(대수 압축 사용)을 보여준다. 바이올린 소리의 경우 연주되는 음의 기본 주파수의 정수배인 고조파(harmonics)에 해당하는 서로 위에 쌓인 수평선을 관찰할 수 있다.
def compute_plot_spectrogram(x, Fs=22050, N=4096, H=2048, ylim=None,
figsize =(5, 2), title='', log=False):
N, H = 1024, 512
X = librosa.stft(y=x, n_fft=N, hop_length=H, win_length=N, window='hann',
center=True, pad_mode='constant')
Y = np.abs(X)**2
if log:
Y_plot = np.log(1 + 100 * Y)
else:
Y_plot = Y
plot_matrix(Y_plot, Fs=Fs/H, Fs_F=N/Fs, title=title, figsize=figsize)
if ylim is not None:
plt.ylim(ylim)
plt.tight_layout()
plt.show()
return Yfn_wav = 'FMP_C8_F02_Long_Violin.wav'
x, Fs = librosa.load(path_data+fn_wav)
Y = compute_plot_spectrogram(x, Fs=Fs, title = 'Violin', ylim=[0, 3000], log=1)
ipd.display(Audio(data=x, rate=Fs))
fn_wav = 'FMP_C8_F02_Long_Castanets.wav'
x, Fs = librosa.load(path_data+fn_wav)
Y = compute_plot_spectrogram(x, Fs=Fs, title = 'Castanets', ylim=[0, 3000], log=1)
ipd.display(Audio(data=x, rate=Fs))
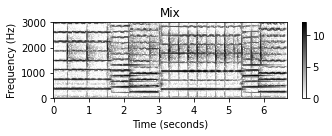
fn_wav = 'FMP_C8_F02_Long_CastanetsViolin.wav'
x, Fs = librosa.load(path_data+fn_wav)
Y = compute_plot_spectrogram(x, Fs=Fs, title = 'Mix', ylim=[0, 3000], log=1)
ipd.display(ipd.Audio(data=x, rate=Fs))
HPS 과정
HPS(Harmonic-Percussive Separation) 의 목표는 주어진 오디오 신호를 두 부분으로 분해하는 것이다. 하나는 화성음로 구성되고 다른 하나는 타악기로 구성된다. 이 작업은 소리의 이벤트가 실제로 화음인지 타악기인지 종종 불분명하기 때문에 다소 모호하다. 실제로 백색소음이나 박수소리 등 화성음도 타악기도 아닌 소리가 많다.
다음 그림에 HPS의 절차가 나와있다. 주어진 신호의 스펙트로그램 표현을 수평 방향(시간에 따라)으로 필터링하여 타악기 이벤트를 억제하면서 하모닉 이벤트를 향상시킨다. 마찬가지로 스펙트로그램은 수직 방향(주파수를 따라)으로 필터링되어 타악기 이벤트를 강화하고 하모닉 이벤트를 억제한다. 2개의 필터링된 스펙트로그램은 시간-주파수(time-frequency) 마스크(mask) 를 생성하는 데 사용되며, 그런 다음 원본 스펙트로그램에 적용된다. 마스킹된 스펙트로그램 표현에서 역 STFT를 적용하여 신호의 하모닉 및 타악기 부분을 얻는다.
Image(path_img+"FMP_C8_F03.png", width=400)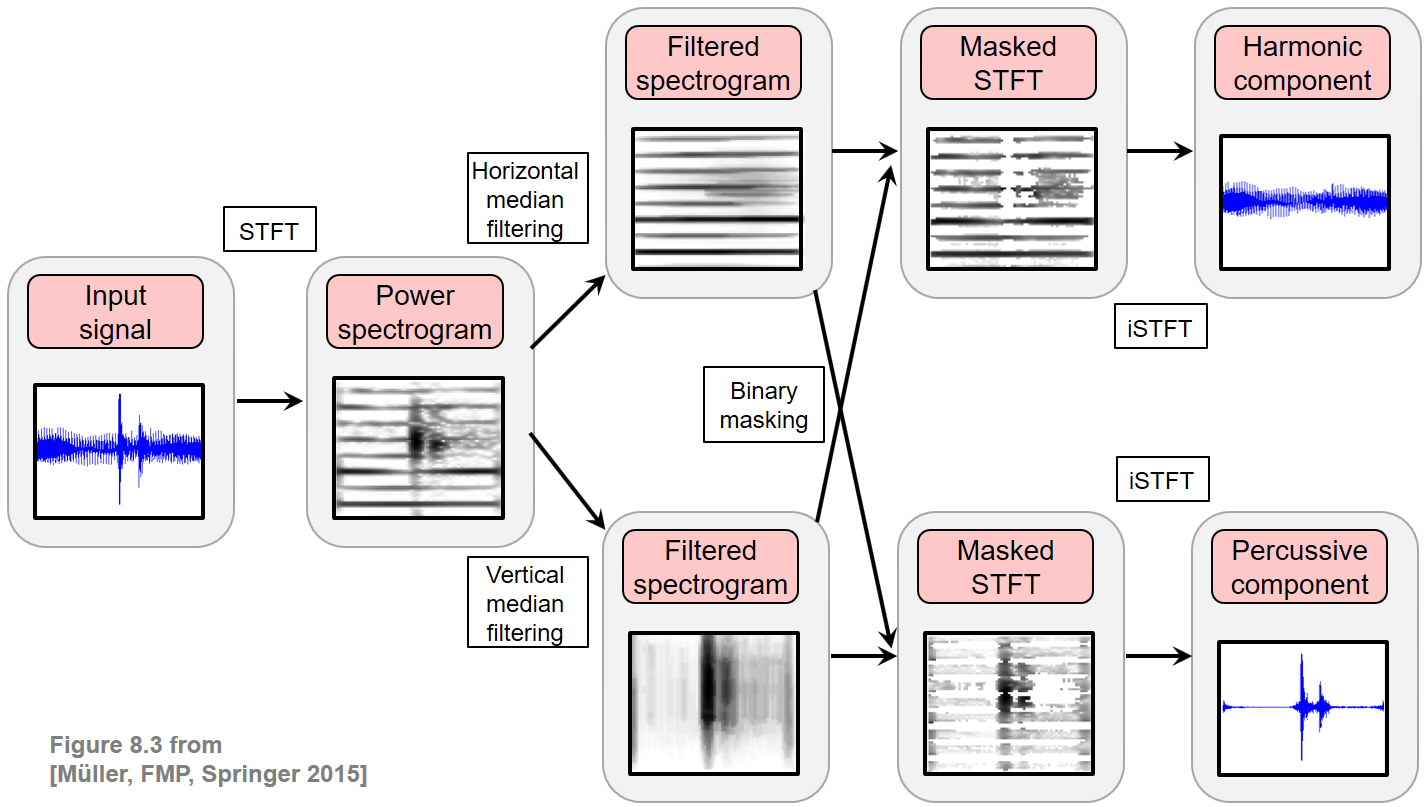
표기법
다음에서 \(x:\mathbb{Z}\to\mathbb{R}\)를 샘플된 오디오 신호의 이산 시간 표현이라고 하자. 목표는 \(x\)를 하모닉 신호 \(x^\mathrm{h}:\mathbb{Z}\to\mathbb{R}\)와 타악기 신호 \(x^\mathrm{p}:\mathbb{Z}\to\mathbb{R}\)로 분해하는 것이다. \[x = x^\mathrm{h} + x^\mathrm{p}\]
첫번째 단계에서 신호 \(x\)의 이산 STFT \(\mathcal{X}\)을 계산한다. 편의를 위해 다음의 정의를 반복한다. \[\mathcal{X}(n,k):= \sum_{r=0}^{N-1} x(r + n H)w(r)\exp(-2\pi ikr/N)\]
- 이 때, \(w:[0:N-1]\to\mathbb{R}\)는 길이 \(N\)과 홉(hop) 크기 매개변수 \(H\)의 적절한 윈도우(window) 함수이다.
이후 단계에서 경계(boundary)에 대한 고려를 피하기 위해 시간 및 주파수 방향에서 행렬 \(\mathcal{X}\)의 적절한 제로 패딩(zero-padding)을 적용하여 \(n\in\mathbb{Z}\) 및 \(k\in\mathbb{Z}\)를 가정할 수 있다. \(\mathcal{X}\)로부터 power 스펙트로그램 \(\mathcal{Y}\)를 도출한다. \[\mathcal{Y}(n,k):= |\mathcal{X}(n,k)|^2\]
중앙값(Median) 필터링
다음 단계에서는 \({\mathcal Y}\)를 필터링하여 하모니 강화(harmonically enhanced) 스펙트로그램 \(\tilde{{\mathcal Y}}_\mathrm{h}\) 및 타악기 강화(percussively enhanced) 스펙트로그램 \(\tilde{{\mathcal Y}}_\mathrm{p}\)를 계산한다.
이를 위해 중앙값 필터링 개념을 적용한다. 유한한 숫자 목록의 중앙값은 숫자의 절반이 값보다 낮고 절반이 그보다 높은 속성을 가진 숫자 값이다.
\(A = (a_1,a_2,\ldots,a_L)\)를 오름차순으로 정렬하면 \(\tilde{A}=(\tilde{a}_1,\tilde{a}_2,\ldots,\tilde{a}_L)\) (\(\ell<m\) , \(\ell,m\in[1:L]\)에 대해 \(\tilde{a}_\ell\leq\tilde{a}_m\))가 생성된다. 그러면 중앙값 \(\mu_{1/2}(A)\)은 다음과 같이 정의된다. \[\mu_{1/2}(A) := \begin{cases}\tilde{a}_{(L+1)/2}, \ \mbox{for $L$ being odd,} \\ (\tilde{a}_{L/2} + \tilde{a}_{L/2+1})/2, \ \mbox{otherwise} \end{cases}\]
중앙값은 실수 시퀀스에 로컬 방식으로 적용될 수 있다. 이를 위해 시퀀스의 주어진 요소를 중앙값으로 대체한다. 이는 \(L\in\mathbb{N}\) 길이의 중앙값 필터 개념으로 이어진다.
\(A=(a_n\mid n\in\mathbb{Z})\)가 실수 \(a_n\in\mathbb{R}\)의 시퀀스이고 \(L\in\mathbb{N}\)가 정수라고 가정한다. 그러면 시퀀스 \(\mu_{1/2}^L[A]\)는 다음과 같이 정의된다. \[\mu_{1/2}^L [A] (n) = \mu_{1/2}\big((a_{n-(L-1)/2},\ldots, a_{n+(L -1)/2})\big)\]
예를 들어 \(A=(\ldots,0,5,3,2,8,2,0,\ldots)\) 시퀀스를 고려해보자. 여기서 \(A\)는 표시된 값을 벗어나면 0이라고 가정한다. \(L=3\)를 사용하여 \(\mu_{1/2}^L[A]=(\ldots,0,3,3,3,2,2,0,\ldots)\)를 얻는다.
scipy-패키지의signal.medfilt함수는 중간 필터를 입력 신호에 적용하며 길이는 매개변수kernel_size(홀수 정수로 가정)에 의해 결정된다. 제로 패딩을 적용하면 출력 신호의 크기가 입력과 동일하다.
A = np.array([5.,3,2,8,2])
filter_len = 3
A_result = signal.medfilt(A, kernel_size=filter_len)
print('A = ', A)
print('A_result = ', A_result)A = [5. 3. 2. 8. 2.]
A_result = [3. 3. 3. 2. 2.]수직 / 수평 중앙값 필터링
이 시나리오에서는 스펙트로그램 \(\mathcal{Y}\)에 중앙값 필터링(median filtering)의 개념을 두가지 방법으로 적용한다. 한번은 \(\mathcal{Y}\)의 행(row)을 고려하여 수평으로, 한번은 \(\mathcal{Y}\)의 열(column)을 고려하여 수직으로 한다.
이렇게 하면 각각 \(\tilde{\mathcal{Y}}^\mathrm{h}\) 및 \(\tilde{\mathcal{Y}}^\mathrm{p}\)로 표시되는 두 개의 필터링된 스펙트로그램이 생성된다.
보다 정확하게는 \(L^\mathrm{h}\) 및 \(L^\mathrm{p}\)를 홀수 길이 매개변수로 두고, 다음을 정의할 수 있다. \[\tilde{\mathcal{Y}}^\mathrm{h}(n,k):=\mu_{1/2}((\mathcal{Y}(n-(L^\mathrm{h}-1)/2,k),\ldots, \mathcal{Y}(n+(L^\mathrm{h}-1)/2,k))),\] \[\tilde{\mathcal{Y}}^\mathrm{p}(n,k):=\mu_{1/2}((\mathcal{Y}(n,k-(L^\mathrm{p}-1)/2),\ldots, \mathcal{Y}(n,k+(L^\mathrm{p}-1)/2)))\] for \(n,k\in\mathbb{Z}\) (\(\mathcal{Y}\)의 제로패딩 가정)
def median_filter_horizontal(x, filter_len):
"""Apply median filter in horizontal direction
Args:
x (np.ndarray): Input matrix
filter_len (int): Filter length
Returns:
x_h (np.ndarray): Filtered matrix
"""
return signal.medfilt(x, [1, filter_len])
def median_filter_vertical(x, filter_len):
"""Apply median filter in vertical direction
Args:
x: Input matrix
filter_len (int): Filter length
Returns:
x_p (np.ndarray): Filtered matrix
"""
return signal.medfilt(x, [filter_len, 1])
def plot_spectrogram_hp(Y_h, Y_p, Fs=22050, N=4096, H=2048, figsize =(10, 2),
ylim=None, clim=None, title_h='', title_p='', log=False):
if log:
Y_h_plot = np.log(1 + 100 * Y_h)
Y_p_plot = np.log(1 + 100 * Y_p)
else:
Y_h_plot = Y_h
Y_p_plot = Y_p
plt.figure(figsize=figsize)
ax = plt.subplot(1,2,1)
plot_matrix(Y_h_plot, Fs=Fs/H, Fs_F=N/Fs, ax=[ax], clim=clim,
title=title_h, figsize=figsize)
if ylim is not None:
ax.set_ylim(ylim)
ax = plt.subplot(1,2,2)
plot_matrix(Y_p_plot, Fs=Fs/H, Fs_F=N/Fs, ax=[ax], clim=clim,
title=title_p, figsize=figsize)
if ylim is not None:
ax.set_ylim(ylim)
plt.tight_layout()
plt.show()- 예를 들어 캐스터네츠 클릭(타악기 성분)이 중첩된 바이올린 녹음(화성 성분)의 예를 보자. 중앙값 필터를 가로 방향으로 적용하면 가로 구조가 더 뚜렷해지고 세로 구조가 사라진다. 수직 방향으로 중앙값 필터를 적용할 경우에도 유사한 개선 효과를 얻을 수 있는데, 이번에는 타악기 구조에 대해 그렇다.
fn_wav = 'FMP_C8_F02_Long_CastanetsViolin.wav'
x, Fs = librosa.load(path_data+fn_wav, mono=True)
N, H = 1024, 512
X = librosa.stft(y=x, n_fft=N, hop_length=H, win_length=N, window='hann', center=True, pad_mode='constant')
Y = np.abs(X)**2
L_set = np.array([[5,5],[23,9],[87,47]])
num = L_set.shape[0]
for m in range(num):
L_h = L_set[m,0]
L_p = L_set[m,1]
Y_h = median_filter_horizontal(Y, L_h)
Y_p = median_filter_vertical(Y, L_p)
title_h = r'Horizontal filtering ($L^h=%d$)'%L_h
title_p = r'Vertical filtering ($L^p=%d$)'%L_p
plot_spectrogram_hp(Y_h, Y_p, Fs=Fs, N=N, H=H,
title_h=title_h, title_p=title_p, ylim=[0, 3000], log=True)


Binary 마스킹, Soft 마스킹
두 개의 필터링된 스펙트로그램 \(\tilde{\mathcal{Y}}^\mathrm{h}\) 및 \(\tilde{\mathcal{Y}}^\mathrm{p}\)는 신호의 하모닉 및 타악기 구성에 직접 적용되지 않는다. 대신 먼저 두 개의 마스크를 생성하는 데 사용되며, 그런 다음 원래 스펙트로그램에서 원하는 구성 요소를 “펀칭 아웃”(“punching out”)하는 데 사용된다.
\(\tilde{\mathcal{Y}}^\mathrm{h}\) 및 \(\tilde{\mathcal{Y}}^\mathrm{p}\)에서 도출할 수 있는 다양한 유형의 시간-주파수 마스크가 있다. 첫 번째 유형은 바이너리 마스크(binary mask)라고 하며 각 시간-주파수 빈에 값 1 또는 값 0이 할당된다. 이진법의 경우 다음을 설정하여 두 마스크를 정의한다. \[\mathcal{M}^\mathrm{h}(n,k) := \begin{cases} 1, & \text{if } \tilde{\mathcal{Y}}^\mathrm{h}(n,k) \geq \tilde{\mathcal{Y}}^\mathrm{p}(n,k), \\ 0, & \text{otherwise,} \end{cases}\] \[\mathcal{M}^\mathrm{p}(n,k) := \begin{cases} 1, & \text{if } \tilde{\mathcal{Y}}^\mathrm{h}(n,k) < \tilde{\mathcal{Y}}^\mathrm{p}(n,k), \\ 0, & \text{otherwise} \end{cases}\]
이분법의 결정 대신 스펙트럼 계수의 크기를 비교할 때 상대적 가중치를 고려할 수 있다. 이는 소프트 마스크(soft mask)라고도 알려진 또 다른 유형의 마스크이다. 이 경우 설정을 통해 두 개의 마스크를 정의한다. \[\mathcal{M}^\mathrm{h}(n,k) := \frac{\tilde{\mathcal{Y}}^\mathrm{h}(n,k)+\varepsilon/2 }{\tilde{\mathcal{Y}}^\mathrm{h}(n,k) +\tilde{\mathcal{Y}}^\mathrm{p}(n,k)+\varepsilon},\] \[\mathcal{M}^\mathrm{p}(n,k) := \frac{\tilde{\mathcal{Y}}^\mathrm{p}(n,k)+\varepsilon/2}{ \tilde{\mathcal{Y}}^\mathrm{h}(n,k) + \tilde{\mathcal{Y}}^\mathrm{p}(n,k)+\varepsilon}\] for \(n,k\in\mathbb{Z}\)
- 0으로 나누지 않도록 작은 양수 \(\varepsilon>0\)를 추가한다.
(바이너리 또는 소프트) 시간-주파수 마스크는 각 시간 주파수 빈이 해당 구성 요소에 속하는 정도를 나타낸다. 구성요소를 얻기 위해 pointwise 곱셈을 통해 원본 스펙트로그램에 마스크를 적용한다. 하모닉 및 타악기 마스크의 경우 두 개의 마스크 버전 \(\mathcal{Y}^\mathrm{h}\) 및 \(\mathcal{Y}^\mathrm{p}\)가 생성되며, 다음과 같이 정의된다. \[\mathcal{Y}^\mathrm{h}(n,k) := \mathcal{M}^\mathrm{h}(n,k) \cdot \mathcal{Y}(n,k),\] \[\mathcal{Y}^\mathrm{p}(n,k) := \mathcal{M}^\mathrm{p}(n,k) \cdot \mathcal{Y}(n,k)\] for \(n,k\in\mathbb{Z}\)
바이너리 마스크의 경우 마스크 값이 1이면 스펙트로그램의 값이 유지되고 마스크 값이 0이면 억제된다. 즉, \(\mathcal{Y}\)의 모든 시간-주파수 빈이 \(\mathcal{Y}^\mathrm{h}\) 또는 \(\mathcal{Y}^\mathrm{p}\)에 할당된다.
소프트 마스크의 경우 이 할당은 마스킹 가중치로 표현된다. 이러한 종류의 스펙트럼 조작은 Wiener 필터링이라고도 하며 통계적 디지털 신호 처리에서 중요한 개념이다.
L_h = 23
L_p = 9
Y_h = median_filter_horizontal(Y, L_h)
Y_p = median_filter_vertical(Y, L_p)
title_h = r'Horizontal filtering ($L^h=%d$)'%L_h
title_p = r'Vertical filtering ($L^p=%d$)'%L_p
plot_spectrogram_hp(Y_h, Y_p, Fs=Fs, N=N, H=H,
title_h=title_h, title_p=title_p, ylim=[0, 3000], log=True)
M_binary_h = np.int8(Y_h >= Y_p)
M_binary_p = np.int8(Y_h < Y_p)
title_h = r'Horizontal binary mask'
title_p = r'Vertical binary mask'
plot_spectrogram_hp(M_binary_h, M_binary_p, Fs=Fs, N=N, H=H, clim=[0,1],
title_h=title_h, title_p=title_p, ylim=[0, 3000])
eps = 0.00001
M_soft_h = (Y_h + eps/2)/(Y_h + Y_p + eps)
M_soft_p = (Y_p + eps/2)/(Y_h + Y_p + eps)
title_h = r'Horizontal soft mask'
title_p = r'Vertical soft mask'
plot_spectrogram_hp(M_soft_h, M_soft_p, Fs=Fs, N=N, H=H, clim=[0,1],
title_h=title_h, title_p=title_p, ylim=[0, 3000])


신호 재구성 (Signal Reconstruction)
지금까지 신호의 스펙트로그램 \(\mathcal{Y}\)를 \(\mathcal{Y}^\mathrm{h}\) 및 \(\mathcal{Y}^\mathrm{p}\) 두 구성요소로 분해했다.
두 개의 시간 영역 신호 \(x^\mathrm{h}\) 및 \(x^\mathrm{p}\)를 얻는 가장 편리한 방법은 두 마스크를 원래 STFT \(\mathcal{X}\)에 직접 적용하여, 2개의 마스킹된 복소수 STFT \(\mathcal{X}^\mathrm{h}\) 및 \(\mathcal{X}^\mathrm{p}\)을 생성하는 것이다.: \[\mathcal{X}^\mathrm{h}(n,k) := \mathcal{M}^\mathrm{h}(n,k) \cdot \mathcal{X}(n,k),\] \[\mathcal{X}^\mathrm{p}(n,k) := \mathcal{M}^\mathrm{p}(n,k) \cdot \mathcal{X}(n,k)\] for \(n,k\in\mathbf{Z}\).
그런 다음 시간 영역 신호 \(x^\mathrm{h}\) 및 \(x^\mathrm{p}\)를 얻기 위해 마스킹된 STFT에 역 STFT를 적용한다. 하지만 몇가지 문제가 있다.
- 첫째, \(\mathcal{X}^\mathrm{h}\) 및 \(\mathcal{X}^\mathrm{p}\) 두 구성 요소에 대해 \(\mathcal{X}\)의 동일한 위상 정보를 사용하는 것은 서로 다른 신호 구성요소 사이의 가능한 위상 간섭(phase interference)에 대해 설명하지 않는다. 일반적으로 서로 다른 신호 구성 요소에 대한 일관된 위상 정보의 추정은 매우 어렵다.
- 두 번째 문제는 STFT 조작(예: 마스크 적용)이 일관된 시간 영역 신호의 재구성에 문제를 일으킬 수 있다는 사실이다. 뒤의 신호 재구성에 대해 더 자세히 다룰 것이다.
다음 예제에서는 바이너리 마스킹의 경우만 고려한다. 마스킹된 STFT에서 신호를 재구성하기 위해
librosa.istft함수를 사용한다.
X_h = X * M_binary_h
X_p = X * M_binary_p
x_h = librosa.istft(X_h, hop_length=H, win_length=N, window='hann', center=True, length=x.size)
x_p = librosa.istft(X_p, hop_length=H, win_length=N, window='hann', center=True, length=x.size)매개변수의 물리적 해석
지금까지 논의된 HPS 절차에는 STFT의 윈도우 길이 \(N\), 홉 크기 \(H\), 중앙값 필터링에 사용되는 필터 길이 \(L^\mathrm{h}\) 및 \(L^\mathrm{p}\) 등 선택해야 할 매개변수가 많다. \(L^\mathrm{h}\) 및 \(L^\mathrm{p}\) 매개변수는 인덱스(즉, 프레임 및 빈)로 지정되었다. 의미 있는 방식으로 이러한 매개변수를 선택하려면 각각 초와 헤르츠 측면에서 물리적 해석을 이해해야 한다.
입력 신호 \(x\)의 샘플링 레이트 \(F_\mathrm{s}\)와 프레임 길이 \(N\) 및 홉 크기 \(H\)가 주어지면 다음 함수는 초 단위로 주어진 필터 길이와 Hertz를 인덱스로 주어진 필터 길이로 변환한다. 중앙값 필터링의 경우 필터 길이가 홀수 정수인지 확인해야 한다.
def convert_l_sec_to_frames(L_h_sec, Fs=22050, N=1024, H=512):
"""Convert filter length parameter from seconds to frame indices
Args:
L_h_sec (float): Filter length (in seconds)
Fs (scalar): Sample rate (Default value = 22050)
N (int): Window size (Default value = 1024)
H (int): Hop size (Default value = 512)
Returns:
L_h (int): Filter length (in samples)
"""
L_h = int(np.ceil(L_h_sec * Fs / H))
return L_h
def convert_l_hertz_to_bins(L_p_Hz, Fs=22050, N=1024, H=512):
"""Convert filter length parameter from Hertz to frequency bins
Args:
L_p_Hz (float): Filter length (in Hertz)
Fs (scalar): Sample rate (Default value = 22050)
N (int): Window size (Default value = 1024)
H (int): Hop size (Default value = 512)
Returns:
L_p (int): Filter length (in frequency bins)
"""
L_p = int(np.ceil(L_p_Hz * N / Fs))
return L_p
def make_integer_odd(n):
"""Convert integer into odd integer
Args:
n (int): Integer
Returns:
n (int): Odd integer
"""
if n % 2 == 0:
n += 1
return nFs, N, H = 22050, 1024, 512
print('L_h(%.1f sec) = %d' % (0.5, make_integer_odd(convert_l_sec_to_frames(0.5, Fs=Fs, N=N, H=H)) ))
print('L_p(%.1f Hz) = %d' % (600, make_integer_odd(convert_l_hertz_to_bins(600, Fs=Fs, N=N, H=H)) ))L_h(0.5 sec) = 23
L_p(600.0 Hz) = 29HPS 구현
- 다음 코드 셀에서는 전체 HPS 절차를 구현하는 함수
hps를 사용한다.
def hps(x, Fs, N, H, L_h, L_p, L_unit='physical', mask='binary', eps=0.001, detail=False):
"""Harmonic-percussive separation (HPS) algorithm
Args:
x (np.ndarray): Input signal
Fs (scalar): Sampling rate of x
N (int): Frame length
H (int): Hopsize
L_h (float): Horizontal median filter length given in seconds or frames
L_p (float): Percussive median filter length given in Hertz or bins
L_unit (str): Adjusts unit, either 'pyhsical' or 'indices' (Default value = 'physical')
mask (str): Either 'binary' or 'soft' (Default value = 'binary')
eps (float): Parameter used in soft maskig (Default value = 0.001)
detail (bool): Returns detailed information (Default value = False)
Returns:
x_h (np.ndarray): Harmonic signal
x_p (np.ndarray): Percussive signal
details (dict): Dictionary containing detailed information; returned if ``detail=True``
"""
assert L_unit in ['physical', 'indices']
assert mask in ['binary', 'soft']
# stft
X = librosa.stft(x, n_fft=N, hop_length=H, win_length=N, window='hann', center=True, pad_mode='constant')
# power spectrogram
Y = np.abs(X) ** 2
# median filtering
if L_unit == 'physical':
L_h = convert_l_sec_to_frames(L_h_sec=L_h, Fs=Fs, N=N, H=H)
L_p = convert_l_hertz_to_bins(L_p_Hz=L_p, Fs=Fs, N=N, H=H)
L_h = make_integer_odd(L_h)
L_p = make_integer_odd(L_p)
Y_h = signal.medfilt(Y, [1, L_h])
Y_p = signal.medfilt(Y, [L_p, 1])
# masking
if mask == 'binary':
M_h = np.int8(Y_h >= Y_p)
M_p = np.int8(Y_h < Y_p)
if mask == 'soft':
eps = 0.00001
M_h = (Y_h + eps / 2) / (Y_h + Y_p + eps)
M_p = (Y_p + eps / 2) / (Y_h + Y_p + eps)
X_h = X * M_h
X_p = X * M_p
# istft
x_h = librosa.istft(X_h, hop_length=H, win_length=N, window='hann', center=True, length=x.size)
x_p = librosa.istft(X_p, hop_length=H, win_length=N, window='hann', center=True, length=x.size)
if detail:
return x_h, x_p, dict(Y_h=Y_h, Y_p=Y_p, M_h=M_h, M_p=M_p, X_h=X_h, X_p=X_p)
else:
return x_h, x_p이제 다양한 매개변수 \(N\), \(H\), \(L^\mathrm{h}\) 및 \(L^\mathrm{p}\)의 역할을 예를 통해 보자. 먼저 다른 설정을 사용하여 HPS 절차를 적용한다. 그런 다음 Chopin의 Prelude Op. 28 No. 4 녹음으로 동일한 실험을 수행한다.
네 가지 매개변수의 상호 작용으로 인해 결과 구성 요소의 음질을 예측하기가 쉽지 않다. \(L^\mathrm{h}\)를 증가시키면 절차가 “하모니적으로 더 엄격해지며” 하모닉에서 타악기 구성 요소로의 “흐름”으로 이어진다. \(L^\mathrm{p}\)를 증가시키면 반대 현상이 발생한다. 음질은 절대값보다 \(L^\mathrm{h}\)와 \(L^\mathrm{p}\) 사이의 상대 관계(relation)에 따라 달라진다. 윈도우 길이 \(N\)도 결정적인 영향을 미친다. 예를 들어 \(N\)을 높이면 하모닉 성분을 분리하는 데 도움이 될 수 있지만 타악기 성분에 “번짐”이 발생합한다.
def generate_audio_tag_html_list(list_x, Fs, width="150", height="40"):
"""Generates audio tag for html needed to be shown in table
Args:
list_x (list): List of waveforms
Fs (scalar): Sample rate
width (str): Width in px (Default value = '150')
height (str): Height in px (Default value = '40')
Returns:
audio_tag_html_list (list): List of HTML strings with audio tags
"""
audio_tag_html_list = []
for i in range(len(list_x)):
audio_tag = ipd.Audio(list_x[i], rate=Fs)
audio_tag_html = audio_tag._repr_html_().replace('\n', '').strip()
audio_tag_html = audio_tag_html.replace('<audio ',
'<audio style="width: '+width+'px; height: '+height+'px;"')
audio_tag_html_list.append(audio_tag_html)
return audio_tag_html_list
def experiment_hps_parameter(fn_wav, param_list):
"""Script for running an HPS experiment over a parameter list, such as ``[[1024, 256, 0.1, 100], ...]``
Args:
fn_wav (str): Path to wave file
param_list (list): List of parameters
"""
Fs = 22050
x, Fs = librosa.load(fn_wav, sr=Fs)
list_x = []
list_x_h = []
list_x_p = []
list_N = []
list_H = []
list_L_h_sec = []
list_L_p_Hz = []
list_L_h = []
list_L_p = []
for param in param_list:
N, H, L_h_sec, L_p_Hz = param
print('N=%4d, H=%4d, L_h_sec=%4.2f, L_p_Hz=%3.1f' % (N, H, L_h_sec, L_p_Hz))
x_h, x_p = hps(x, Fs=Fs, N=N, H=H, L_h=L_h_sec, L_p=L_p_Hz)
L_h = convert_l_sec_to_frames(L_h_sec=L_h_sec, Fs=Fs, N=N, H=H)
L_p = convert_l_hertz_to_bins(L_p_Hz=L_p_Hz, Fs=Fs, N=N, H=H)
list_x.append(x)
list_x_h.append(x_h)
list_x_p.append(x_p)
list_N.append(N)
list_H.append(H)
list_L_h_sec.append(L_h_sec)
list_L_p_Hz.append(L_p_Hz)
list_L_h.append(L_h)
list_L_p.append(L_p)
html_x = generate_audio_tag_html_list(list_x, Fs=Fs)
html_x_h = generate_audio_tag_html_list(list_x_h, Fs=Fs)
html_x_p = generate_audio_tag_html_list(list_x_p, Fs=Fs)
pd.options.display.float_format = '{:,.1f}'.format
pd.set_option('display.max_colwidth', None)
df = pd.DataFrame(OrderedDict([
('$N$', list_N),
('$H$', list_H),
('$L_h$ (sec)', list_L_h_sec),
('$L_p$ (Hz)', list_L_p_Hz),
('$L_h$', list_L_h),
('$L_p$', list_L_p),
('$x$', html_x),
('$x_h$', html_x_h),
('$x_p$', html_x_p)]))
df.index = np.arange(1, len(df) + 1)
ipd.display(ipd.HTML(df.to_html(escape=False, index=False))) param_list = [
[1024, 256, 0.1, 100],
[1024, 256, 0.1, 1000],
[1024, 256, 0.8, 100],
[8192, 256, 0.1, 100]] fn_wav = 'FMP_C8_F02_Long_CastanetsViolin.wav'
print('=============================================================')
print('Experiment for ',"Castanets Violin")
experiment_hps_parameter(path_data+fn_wav, param_list)
fn_wav = 'FMP_C8_F27_Chopin_Op028-04_minor.wav'
#print('=============================================================')
#print('Experiment for ',"Chopin Op28-04", param_list)
#experiment_hps_parameter(path_data+fn_wav, param_list) =============================================================
Experiment for Castanets Violin
N=1024, H= 256, L_h_sec=0.10, L_p_Hz=100.0
N=1024, H= 256, L_h_sec=0.10, L_p_Hz=1000.0
N=1024, H= 256, L_h_sec=0.80, L_p_Hz=100.0
N=8192, H= 256, L_h_sec=0.10, L_p_Hz=100.0| $N$ | $H$ | $L_h$ (sec) | $L_p$ (Hz) | $L_h$ | $L_p$ | $x$ | $x_h$ | $x_p$ |
|---|---|---|---|---|---|---|---|---|
| 1024 | 256 | 0.1 | 100 | 9 | 5 | |||
| 1024 | 256 | 0.1 | 1000 | 9 | 47 | |||
| 1024 | 256 | 0.8 | 100 | 69 | 5 | |||
| 8192 | 256 | 0.1 | 100 | 9 | 38 |
# 다른 예시
def experiment_hps_pieces(wav_list, path, piece_list,
Fs = 22050, N=1024, H=256, L_h_sec=0.2, L_p_Hz=500):
"""Script for running experiment over list of different pieces
"""
list_x = []
list_x_h = []
list_x_p = []
for wav in wav_list:
print(wav)
x, Fs = librosa.load(path_data+wav, sr=Fs)
x_h, x_p = hps(x, Fs=Fs, N=N, H=H, L_h=L_h_sec, L_p=L_p_Hz)
list_x.append(x)
list_x_h.append(x_h)
list_x_p.append(x_p)
html_x = generate_audio_tag_html_list(list_x, Fs=Fs)
html_x_h = generate_audio_tag_html_list(list_x_h, Fs=Fs)
html_x_p = generate_audio_tag_html_list(list_x_p, Fs=Fs)
pd.options.display.float_format = '{:,.1f}'.format
pd.set_option('display.max_colwidth', None)
df = pd.DataFrame(OrderedDict([
('Piece', piece_list),
('x', html_x),
('x_h', html_x_h),
('x_p', html_x_p)]))
df.index = np.arange(1, len(df) + 1)
ipd.display(ipd.HTML(df.to_html(escape=False, index=False))) wav_list = (
'FMP_C8_F02_Long_CastanetsViolinApplause.wav',
'FMP_C8_F02_VibratoImpulsesNoise.wav',
'FMP_C8_Audio_Bornemark_StopMessingWithMe-Excerpt_SoundCloud_mix.wav'
)
piece_list = (
'Violin + Castanets + Applause',
'Vibrato + Impulses + Noise',
'Bornemark, Stop Messing With Me'
)
#experiment_hps_pieces(wav_list, path_data, piece_list)Harmonic–Residual–Percussive Separation (HRPS)
HPS의 기본 가정은 스펙트로그램에서 화성음은 수평 구조에 해당하고 타악기음은 수직 구조에 해당한다는 것이다. 그러나 수평적 구조도 수직적 구조에도 해당되지 않는 소리가 많이 있다. 예를 들어, 박수 소리나 왜곡된 기타와 같은 잡음과 같은 소리는 명확한 구조 없이 전체 스펙트로그램에 걸쳐 많은 푸리에 계수가 분포된다. HPS 절차를 적용할 때 이러한 소음과 같은 구성 요소는 부분적으로는 화성음에 부분적으로는 타악기 부분에 무작위로 할당될 수 있다.
명확한 화성 요소와 명확한 타악기 요소 사이에 있는 소리를 캡처하는 세 번째 잔여(residual) 요소를 고려하여 HPS에 대한 확장을 본다. 그 절차는 Harmonic-Residual-Percussive Separation(HRPS)이라고도 한다.
Image(path_img+"FMP_C8_E05_HRP.png", width=400)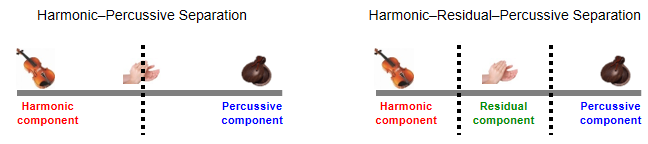
- \(x:\mathbb{Z}\to\mathbb{R}\)를 입력 신호라고 하자. 목표는 \(x\)를 화성 성분 신호 \(x^\mathrm{h}\), 잔류 성분 신호 \(x^\mathrm{r}\) 및 타악기 성분 신호 \(x^\mathrm{p}\)로 분해하는 것이다.
- $x = x^ + x^ + x^. $
Image(path_img+"FMP_C8_E05_HRP-color.png", width=400)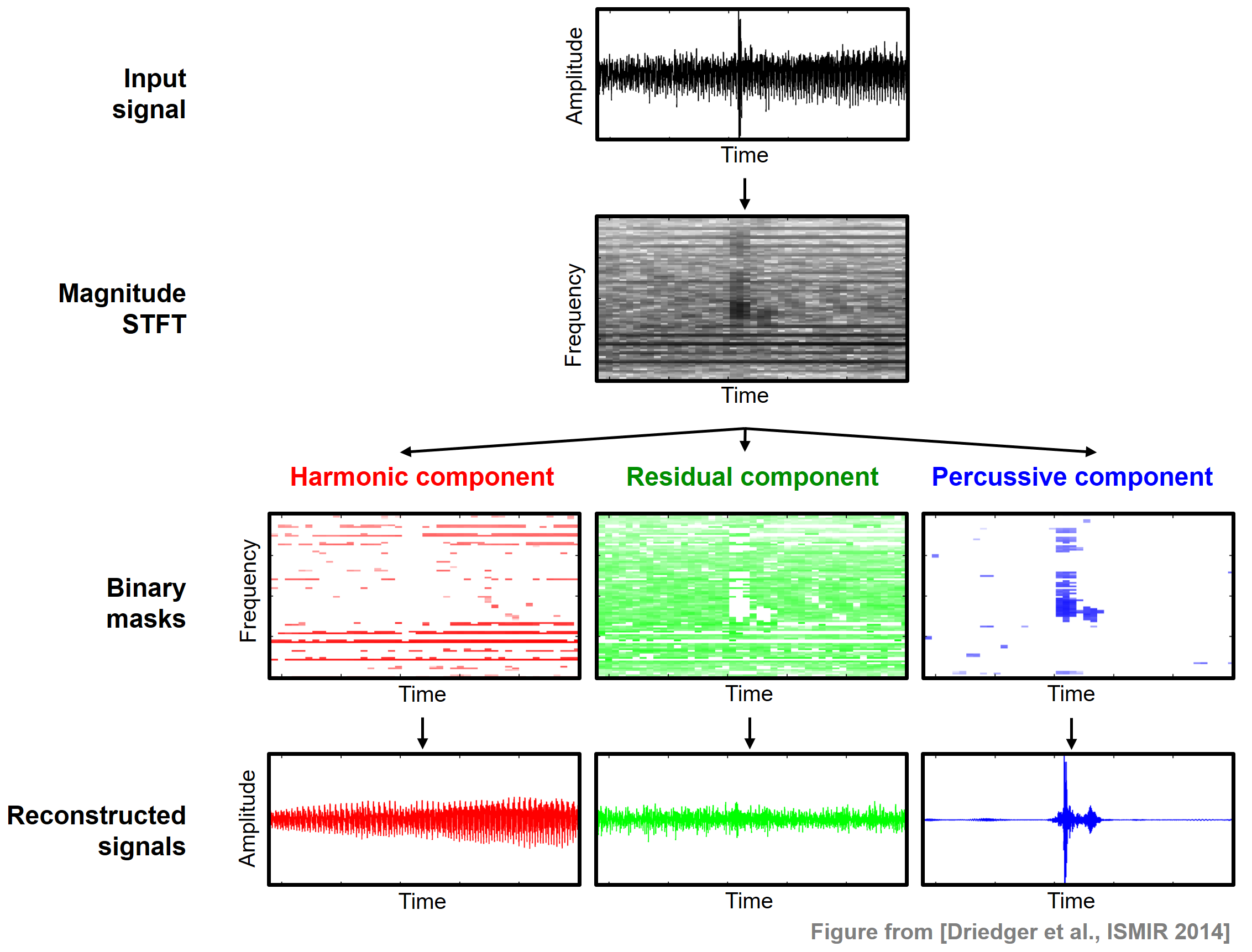
먼저 신호 \(x\)가 크기 스펙트로그램 \(\mathcal{Y}\)로 변환된다. \(\tilde{\mathcal{Y}}^\mathrm{h}\) 및 \(\tilde{\mathcal{Y}}^\mathrm{p}\)을 얻기 위해 중앙값 필터링을 수평으로 한 번, 수직으로 한 번 적용한다. 중앙값 필터링의 경우 \(L^\mathrm{h}\) 및 \(L^\mathrm{p}\)를 홀수 길이 매개변수로 둔다. 잔차 성분을 정의하기 위해 분리 계수(separation factor) 라고 하는 \(\beta \geq 1\)가 있는 추가 매개변수 \(\beta\in\mathbb{R}\)를 고려한다.
HPS에서 사용되는 바이너리 마스크의 정의를 일반화하면 바이너리 마스크 \(\mathcal{M}^\mathrm{h}\), \(\mathcal{M}^\mathrm{r}\) 및 \(\mathcal{M}^\mathrm{p}\)를 각각 명확한 화성, 명확한 타악기, 잔여 성분으로 정의하며 다음과 같이 설정한다.
\[ \mathcal{M}^\mathrm{h}(n,k) := \begin{cases} 1 & \text{if } \tilde{\mathcal{Y}}^\mathrm{h}(n,k) \geq \beta\cdot \tilde{\mathcal{Y}}^\mathrm{p}(n,k), \\ 0 & \text{otherwise,} \end{cases}\] \[\mathcal{M}^\mathrm{p}(n,k) := \begin{cases} 1 & \text{if } \tilde{\mathcal{Y}}^\mathrm{p}(n,k) > \beta\cdot \tilde{\mathcal{Y}}^\mathrm{h}(n,k), \\ 0 & \text{otherwise,} \end{cases}\] \[\mathcal{M}^\mathrm{r}(n,k) := 1 - \big( \mathcal{M}^\mathrm{h}(n,k) + \mathcal{M}^\mathrm{p}(n,k) \big)\]
이러한 마스크르 사용하여 다음을 정의한다. \[\mathcal{X}^\mathrm{h}(n,k) := \mathcal{M}^\mathrm{h}(n,k) \cdot \mathcal{X}(n,k),\] \[\mathcal{X}^\mathrm{p}(n,k) := \mathcal{M}^\mathrm{p}(n,k) \cdot \mathcal{X}(n,k),\] \[\mathcal{X}^\mathrm{r}(n,k) := \mathcal{M}^\mathrm{r}(n,k) \cdot \mathcal{X}(n,k)\] for \(n,k\in\mathbf{Z}\).
마지막으로 역 STFT를 적용하여 시간 영역 신호 \(x^\mathrm{h}\), \(x^\mathrm{p}\) 및 \(x^\mathrm{r}\)를 도출할 수 있다. 다음 함수
HRPS는 이 절차를 구현한다.
def hrps(x, Fs, N, H, L_h, L_p, beta=2.0, L_unit='physical', detail=False):
"""Harmonic-residual-percussive separation (HRPS) algorithm
Args:
x (np.ndarray): Input signal
Fs (scalar): Sampling rate of x
N (int): Frame length
H (int): Hopsize
L_h (float): Horizontal median filter length given in seconds or frames
L_p (float): Percussive median filter length given in Hertz or bins
beta (float): Separation factor (Default value = 2.0)
L_unit (str): Adjusts unit, either 'pyhsical' or 'indices' (Default value = 'physical')
detail (bool): Returns detailed information (Default value = False)
Returns:
x_h (np.ndarray): Harmonic signal
x_p (np.ndarray): Percussive signal
x_r (np.ndarray): Residual signal
details (dict): Dictionary containing detailed information; returned if "detail=True"
"""
assert L_unit in ['physical', 'indices']
# stft
X = librosa.stft(x, n_fft=N, hop_length=H, win_length=N, window='hann', center=True, pad_mode='constant')
# power spectrogram
Y = np.abs(X) ** 2
# median filtering
if L_unit == 'physical':
L_h = convert_l_sec_to_frames(L_h_sec=L_h, Fs=Fs, N=N, H=H)
L_p = convert_l_hertz_to_bins(L_p_Hz=L_p, Fs=Fs, N=N, H=H)
L_h = make_integer_odd(L_h)
L_p = make_integer_odd(L_p)
Y_h = signal.medfilt(Y, [1, L_h])
Y_p = signal.medfilt(Y, [L_p, 1])
# masking
M_h = np.int8(Y_h >= beta * Y_p)
M_p = np.int8(Y_p > beta * Y_h)
M_r = 1 - (M_h + M_p)
X_h = X * M_h
X_p = X * M_p
X_r = X * M_r
# istft
x_h = librosa.istft(X_h, hop_length=H, win_length=N, window='hann', center=True, length=x.size)
x_p = librosa.istft(X_p, hop_length=H, win_length=N, window='hann', center=True, length=x.size)
x_r = librosa.istft(X_r, hop_length=H, win_length=N, window='hann', center=True, length=x.size)
if detail:
return x_h, x_p, x_r, dict(Y_h=Y_h, Y_p=Y_p, M_h=M_h, M_r=M_r, M_p=M_p, X_h=X_h, X_r=X_r, X_p=X_p)
else:
return x_h, x_p, x_rHPRS 구현
이제 위의 바이올린, 박수, 캐스터네츠 녹음을 중첩하여 HRPS 절차를 시도한다. 다음 그림은 바이너리 마스크 \(\mathcal{M}^\mathrm{h}\), \(\mathcal{M}^\mathrm{r}\) 및 \(\mathcal{M}^\mathrm{p}\)를 보여준다.
화성 신호 \(x^\mathrm{h}\)는 대부분 바이올린에 해당하는 반면 나머지 신호 \(x^\mathrm{r}\)는 박수 소리의 대부분을 포착한다. 타악기 신호 \(x^\mathrm{p}\)에는 캐스터네츠가 포함되어 있지만 신호가 상당히 왜곡되어 있으며 여전히 많은 박수 성분이 포함되어 있다. 신호 왜곡의 또 다른 이유는 신호 재구성 단계에서 도입된 위상 아티팩트(phase artifacts) 때문이기도 하다. 이러한 아티팩트는 특히 타악기 구성 요소에서 들을 수 있다.
fn_wav ='FMP_C8_F02_Long_CastanetsViolinApplause.wav'
x, Fs = librosa.load(path_data+fn_wav)
N = 1024
H = 512
L_h_sec = 0.2
L_p_Hz = 500
beta = 2
x_h, x_p, x_r, D = hrps(x, Fs=Fs, N=N, H=H,
L_h=L_h_sec, L_p=L_p_Hz, beta=beta, detail=True)ylim = [0, 3000]
plt.figure(figsize=(10,3))
ax = plt.subplot(1,3,1)
plot_matrix(D['M_h'], Fs=Fs/H, Fs_F=N/Fs, ax=[ax], clim=[0,1],
title='Horizontal binary mask')
ax.set_ylim(ylim)
ax = plt.subplot(1,3,2)
plot_matrix(D['M_r'], Fs=Fs/H, Fs_F=N/Fs, ax=[ax], clim=[0,1],
title='Residual binary mask')
ax.set_ylim(ylim)
ax = plt.subplot(1,3,3)
plot_matrix(D['M_p'], Fs=Fs/H, Fs_F=N/Fs, ax=[ax], clim=[0,1],
title='Vertical binary mask')
ax.set_ylim(ylim)
plt.tight_layout()
plt.show()
html_x_h = generate_audio_tag_html_list([x_h], Fs=Fs, width='220')
html_x_r = generate_audio_tag_html_list([x_r], Fs=Fs, width='220')
html_x_p = generate_audio_tag_html_list([x_p], Fs=Fs, width='220')
pd.options.display.float_format = '{:,.1f}'.format
pd.set_option('display.max_colwidth', None)
df = pd.DataFrame(OrderedDict([
('$x_h$', html_x_h),
('$x_r$', html_x_r),
('$x_p$', html_x_p)]))
ipd.display(ipd.HTML(df.to_html(escape=False, header=False, index=False)))
분리 계수(separation factor)의 영향
분리 계수 \(\beta\)는 분해를 조정하는 데 사용할 수 있다. \(\beta=1\)의 경우는 원래의 HP 분해로 축소된다. \(\beta\)를 증가시키면 \(x^\mathrm{h}\) 및 \(x^\mathrm{p}\) 구성 요소의 재구성에 더 적은 시간-주파수 빈이 할당되는 반면, 더 많은 시간-주파수 빈이 잔차 성분 \(x^\mathrm{r}\)의 재구성에 사용된다.
직관적으로 \(\beta\) 매개변수가 클수록 \(x^\mathrm{h}\) 및 \(x^\mathrm{p}\) 구성 요소의 화성 및 타악기 특성이 더 명확해진다. 매우 큰 \(\beta\)의 경우 잔차 신호 \(x^\mathrm{r}\)는 전체 신호 \(x\)를 포함하는 경향이 있다.
Image(path_img+"FMP_C8_E05_HRP_beta.png", width=500)
def experiment_hrps_parameter(fn_wav, param_list):
"""Script for running an HRPS experiment over a parameter list, such as ``[[1024, 256, 0.1, 100], ...]``
Args:
fn_wav (str): Path to wave file
param_list (list): List of parameters
"""
x, Fs = librosa.load(fn_wav)
list_x = []
list_x_h = []
list_x_p = []
list_x_r = []
list_N = []
list_H = []
list_L_h_sec = []
list_L_p_Hz = []
list_L_h = []
list_L_p = []
list_beta = []
for param in param_list:
N, H, L_h_sec, L_p_Hz, beta = param
print('N=%4d, H=%4d, L_h_sec=%4.2f, L_p_Hz=%3.1f, beta=%3.1f' % (N, H, L_h_sec, L_p_Hz, beta))
x_h, x_p, x_r = hrps(x, Fs=Fs, N=1024, H=512, L_h=L_h_sec, L_p=L_p_Hz, beta=beta)
L_h = convert_l_sec_to_frames(L_h_sec=L_h_sec, Fs=Fs, N=N, H=H)
L_p = convert_l_hertz_to_bins(L_p_Hz=L_p_Hz, Fs=Fs, N=N, H=H)
list_x.append(x)
list_x_h.append(x_h)
list_x_p.append(x_p)
list_x_r.append(x_r)
list_N.append(N)
list_H.append(H)
list_L_h_sec.append(L_h_sec)
list_L_p_Hz.append(L_p_Hz)
list_L_h.append(L_h)
list_L_p.append(L_p)
list_beta.append(beta)
html_x = generate_audio_tag_html_list(list_x, Fs=Fs)
html_x_h = generate_audio_tag_html_list(list_x_h, Fs=Fs)
html_x_p = generate_audio_tag_html_list(list_x_p, Fs=Fs)
html_x_r = generate_audio_tag_html_list(list_x_r, Fs=Fs)
pd.options.display.float_format = '{:,.1f}'.format
pd.set_option('display.max_colwidth', None)
df = pd.DataFrame(OrderedDict([
('$N$', list_N),
('$H$', list_H),
('$L_h$ (sec)', list_L_h_sec),
('$L_p$ (Hz)', list_L_p_Hz),
('$L_h$', list_L_h),
('$L_p$', list_L_p),
('$\\beta$', list_beta),
('$x$', html_x),
('$x_h$', html_x_h),
('$x_r$', html_x_r),
('$x_p$', html_x_p)]))
df.index = np.arange(1, len(df) + 1)
ipd.display(ipd.HTML(df.to_html(escape=False, index=False)))param_list = [
[1024, 256, 0.2, 500, 1.1],
[1024, 256, 0.2, 500, 2],
[1024, 256, 0.2, 500, 4],
[1024, 256, 0.2, 500, 32],
]
fn_wav = 'FMP_C8_F02_Long_CastanetsViolinApplause.wav'
print('=============================================================')
print('Experiment for ',"Castanets Violin Applause")
experiment_hrps_parameter(path_data+fn_wav, param_list)=============================================================
Experiment for Castanets Violin Applause
N=1024, H= 256, L_h_sec=0.20, L_p_Hz=500.0, beta=1.1
N=1024, H= 256, L_h_sec=0.20, L_p_Hz=500.0, beta=2.0
N=1024, H= 256, L_h_sec=0.20, L_p_Hz=500.0, beta=4.0
N=1024, H= 256, L_h_sec=0.20, L_p_Hz=500.0, beta=32.0| $N$ | $H$ | $L_h$ (sec) | $L_p$ (Hz) | $L_h$ | $L_p$ | $\beta$ | $x$ | $x_h$ | $x_r$ | $x_p$ |
|---|---|---|---|---|---|---|---|---|---|---|
| 1024 | 256 | 0.2 | 500 | 18 | 24 | 1.1 | ||||
| 1024 | 256 | 0.2 | 500 | 18 | 24 | 2.0 | ||||
| 1024 | 256 | 0.2 | 500 | 18 | 24 | 4.0 | ||||
| 1024 | 256 | 0.2 | 500 | 18 | 24 | 32.0 |
Cascaded HRPS
HRPS 절차는 더 확장될 수 있다.예를 들어, cascaded harmonic-residual-percussive(CHRPS) 절차가 있다.
먼저 큰 분리 계수(예: \(\beta=5\))를 사용하여 신호를 화성(H), 잔차(R) 및 타악기(P) 성분으로 분리한다. 그런 다음 더 작은 분리 계수(예: \(\beta=3\))를 사용하여 첫 번째 단계의 잔차 성분을 추가로 구성한다.
보다 일반적으로, 분리 계수 \(\beta_1 > \beta_2 > \ldots >\beta_B\)가 감소하는 \(B\in\mathbb{R}\) 계단식 단계를 사용하여 CHRP 절차는 \((2B+1)\) 구성요소 신호를 생성한다. 합계는 입력 신호 \(x\)와 같다(작은 오류까지).
필요한 모든 계단식 단계가 완료되면 각 요소의 신호가 화성에서 잔차를 거쳐 타악기 순으로 축에 정렬된다.
다음 그림은 \(B = 3\)를 사용하여 이 절차를 보여준다. 이 경우 CHRP 절차는 H, RH, RRH, RRR, RRP, RP, P의 7개의 구성 요소 신호를 생성한다.
Image(path_img+"FMP_C8_E05_HRP-cascaded.png", width=400)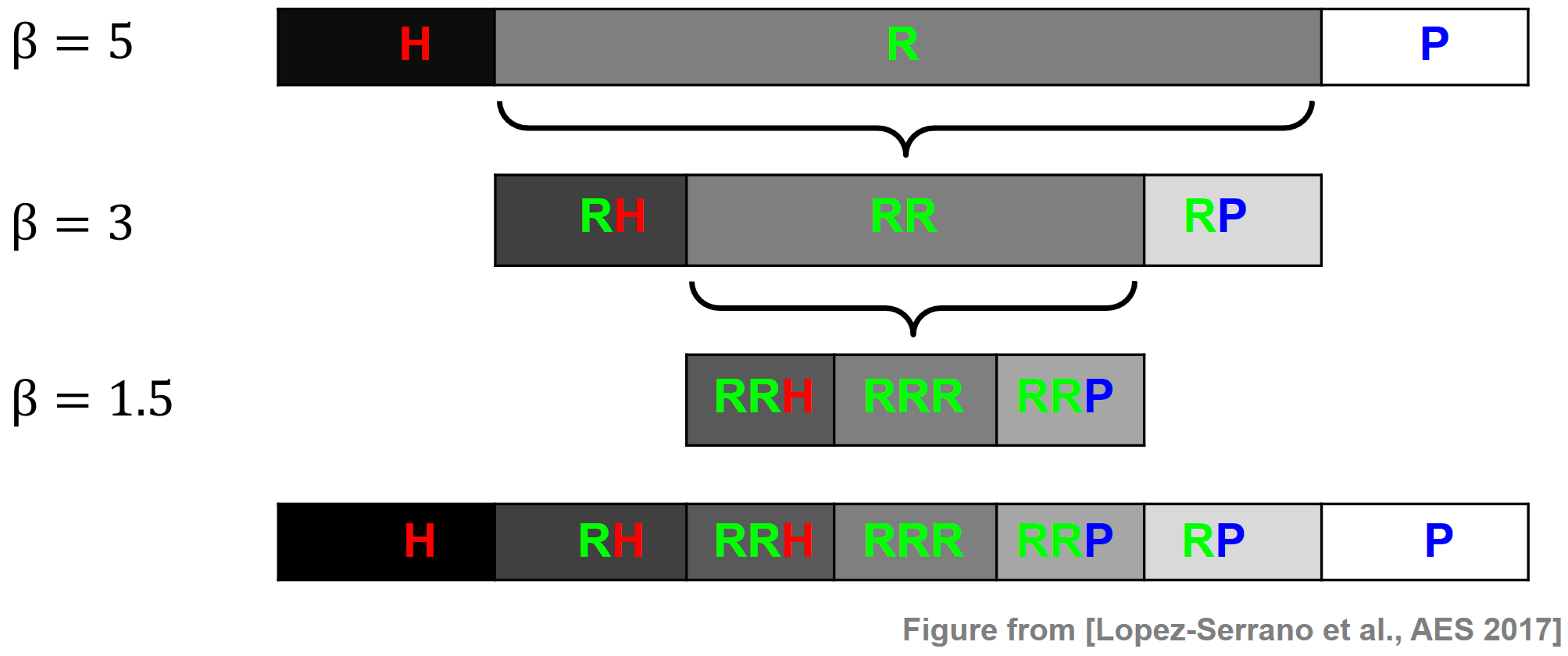
CHRP 피쳐
음악 이벤트 밀도(density) 및 음악 구조 분석과 같은 작업 등으로부터 동기를 부여받아 이제 중간-수준(mid-level) 특징 표현을 소개한다.
이를 위해 슬라이딩 윈도우 기법을 사용하여 \(2B+1\) 성분 신호 각각에 대한 로컬 에너지를 계산한다. 이를 위해 윈도우 길이가 \(N\in\mathbb{N}\)이고 홉 크기 \(H\in\mathbb{N}\)를 사용한다.
\(M\in\mathbb{N}\)을 에너지 프레임의 수라고 한다. 그런 다음, 모든 구성 요소 신호의 로컬 에너지 값을 \(m\in[1:M]\)에 대해 \(v_m\in\mathbb{R}^{2B+1}\)가 되도록 특징 행렬 \(V=(v_1,\ldots,v_M)\)에 쌓는다. 또한 \(v_m\) 열은 (예: \(\ell^1\)-norm)을 사용하여 정규화될 수 있다.
각 \(v_m\in[0,1]^{2B+1}\)는 각 프레임 \(m\in[1:M]\)에 대한 구성요소 전체의 에너지 분포를 나타낸다.
다음 예에서는 겹치지 않는 5개의 사운드 샘플(캐스터네츠, 스네어 롤, 박수, 스타카토 현 및 레가토 바이올린)로 구성된 신호에 대한 CHRP 특징 매트릭스를 보여준다.
캐스터네츠는 충격 에너지가 가장 높고 P 성분에 잘 국한되어 있다. 스네어 롤은 주로 RP와 RRR로 구성된다. 실제로 스네어 드럼은 타악기적인 어택과 시끄럽고 음색이 강한 감쇠 곡선(드럼의 튜닝 주파수에 따라 다름)을 가지고 있다. 빠르게 연속적으로 치면 노이지한 디케이(decay) 꼬리가 타악기 온셋보다 우세하다. 박수는 RRR을 중심으로 하며 잔여 영역에 잘 국한된다. 스타카토 현은 이 연주 기법에서 나타나는 시끄러운 공격에 해당하는 추가 RH 구성 요소와 함께 주로 하모닉하다. 바이올린 레가토는 H 구성 요소로 제한된다. 안정적인 화성 신호 특성이 다른 모든 구성 요소를 지배하기 때문이다.
ipd.display(Image(path_img+ "FMP_C8_E05_CHRP_Ex-Ramp.png", width=400))
# ipd.display(Audio(path_data+"FMP_C8_PLS-Fig-5-2_PRH-RampSynthetic.wav"))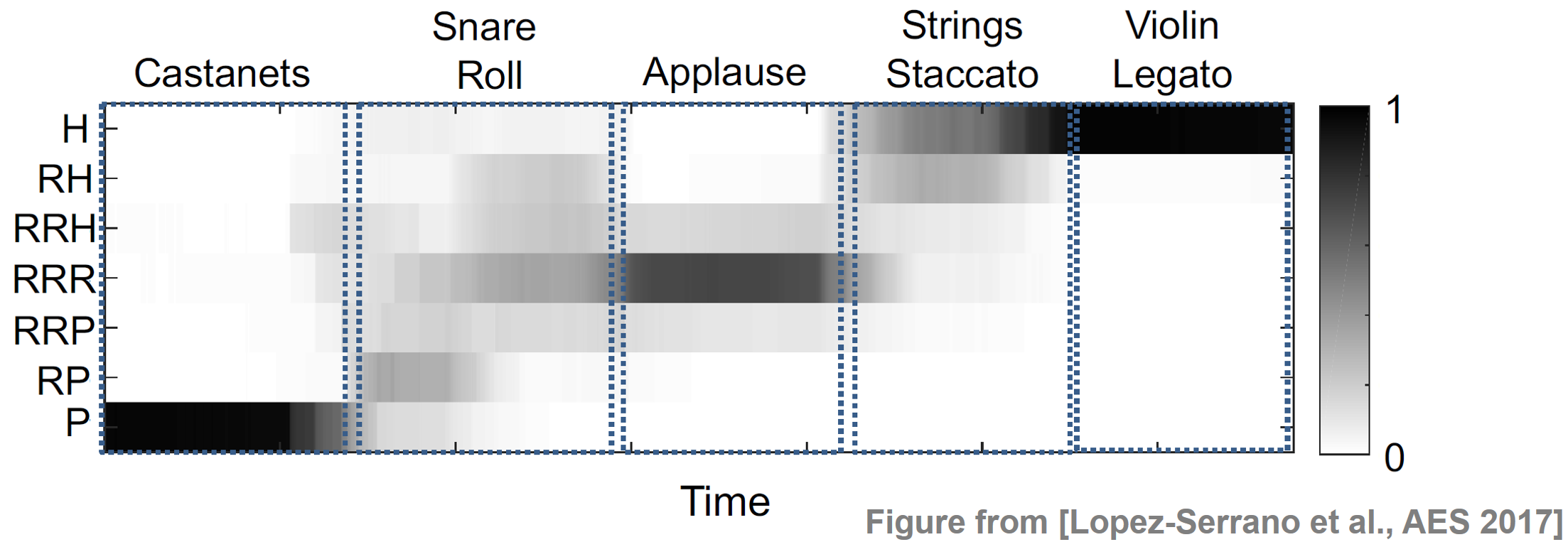
다음 예는 패러디들(paradiddles) 이라고 알려진 스네어 연주 기법에서 타악기에서 잔차로 에너지가 이동하는 것을 보여준다. 다음 그림에서는 스네어 드럼에서 연주되는 패러디들의 파형을 보여준다.
처음에 속도가 증가(\(0\)-\(40\) 초)하고 그 다음 속도가 감소(\(40\)-\(75\) 초)하는 연주이다. 결과 CHRP 특징 행렬에서 특정 온셋 주파수 또는 재생 속도에 도달(약 \(25\)초 즈음)한 후 남은 P 에너지가 얼마나 적은지 알 수 있다. 이것은 소음과 같은 꼬리가 상대적 근접에 도달하고 개별 타악기 온셋을 압도하여 특징 행렬의 나머지 구성 요소 주위에 에너지를 집중시키기 때문이다.
ipd.display(Image(path_img+ "FMP_C8_E05_CHRP_Ex-Snare.png", width=400))
#ipd.display(Audio(path_data+"FMP_C8_PLS-Fig-5-3_Paradiddle.wav"))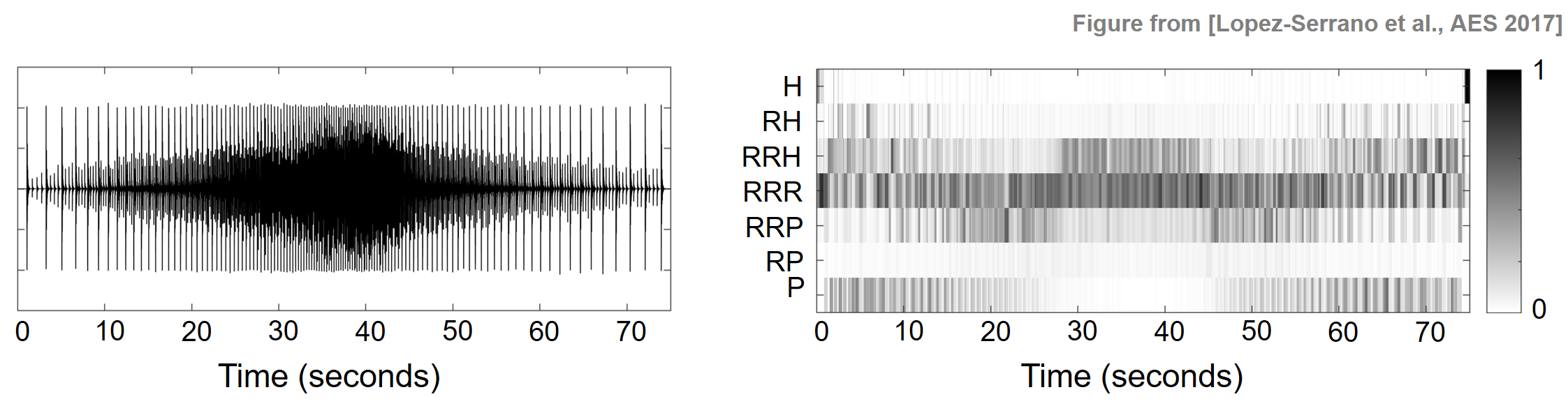
신호 재구성 (Signal Reconstruction)
하모닉-타악기 분리 절차에서 첫 번째 단계는 STFT를 사용하여 음악 신호를 시간-주파수 표현으로 변환하는 것이었다. 그런 다음 적절한 마스킹 기술을 적용하여 시간-주파수 표현을 조작하여 수정된(modified) STFT(MSTFT)를 생성했다. 마지막으로 역 STFT를 적용하여 수정된 STFT를 다시 시간 영역으로 변환했다. 이러한 접근 방식은 간단해 보이지만 수정된 STFT 표현에서 시간 영역 신호를 재구성하는 데 예상치 못한 몇 가지 위험이 있다.
한 가지 중요한 질문은 STFT가 지정된 MSTFT와 일치하는 시간 영역 신호가 있는지 여부이다. 이 경우 MSTFT가 유효하다고 말한다. 그러나 실제로는 대부분의 수정된 STFT가 유효하지 않은 것으로 나타났다.
다음에서는 실제로 수정된 STFT에서 일반적으로 신호를 재구성하는 방법을 설명하고 이 절차의 단점에 대해 설명한다.
표기 및 문제 공식
\(x:\mathbb{Z}\to\mathbb{R}\)를 이산 시간 신호라고 하고, \(\mathcal{X}\)를 \(N\in\mathbb{N}\) 길이의 윈도우 함수 \(w:[0:N-1]\to\mathbb{R}\)와 홉 크기 매개변수 \(H\in\mathbb{N}\)에 기반한 STFT라고 하자.
원래 신호는 조건 \(\sum_{n\in\mathbb{Z}} w(r-nH)\not= 0\)가 성립할 때 \(\mathcal{X}\)로부터 완벽하게 재구성할 수 있다. \(\mathcal{X}^\mathrm{mod}\)가 주어진 MSTFT라고 가정하자. 수정된 경우의 재구성에서 다음 절차를 적용하는 것이 간단해 보인다. 첫 번째 단계에서 \(\mathcal{X}^\mathrm{mod}\)의 각 열에 역 DFT를 적용하여 다음의 결과를 얻는다. \[(v_n(0),\ldots, v_n(N-1))^\top := \mathrm{DFT}_N^{-1} \Big((\mathcal{X}^\mathrm{mod}(n, 0),\ldots, \mathcal{X}^\mathrm{mod}d(n,N-1))^\top\Big)\] for \(n\in\mathbb{Z}\)
또한 \(r\in\mathbb{Z}\setminus[0:N-1]\)에 대해 \(v_n(r):=0\)로 설정한다. 그런 다음 중첩-추가(overlap-add) 기술을 적용하여 \(x^\mathrm{Rec}:\mathbb{Z}\to\mathbb{R}\) 신호를 다음과 같이 설정하여 정의한다. \[x^\mathrm{Rec}(r) := \frac{\sum_{n\in\mathbb{Z}} v_n(r-nH)}{\sum_{n\in\mathbb{Z}} w(r-nH)}\] for \(r\in\mathbb{Z}\).
신호 \(x^\mathrm{Rec}\)에는 문제가 있다. 일반적으로 신호 \(x^\mathrm{Rec}\)의 STFT \(\mathcal{X}^\mathrm{Rec}\)는 수정된 STFT \(\mathcal{X}^\mathrm{mod}\)와 동일하지 않다. 그 이유는 \(x^\mathrm{Rec}\)에 윈도우잉을 적용할 때 결과적으로 윈도우화된 섹션 \(x^\mathrm{Rec}_n\)이 일반적으로 \(v_n\)과 일치하지 않기 때문이다.
예시
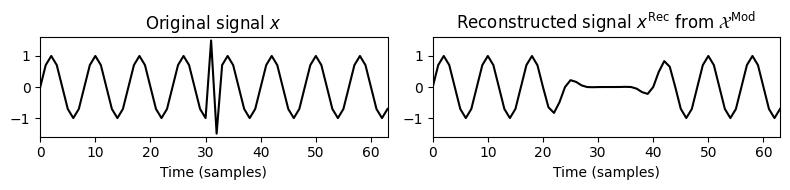
- 이 상황은 다음 그림으로 설명된다. 첫 번째 행에는 신호 \(x\), 세 개의 윈도우 섹션 \(x_n\) 및 크기(magnitude) STFT의 결과 열이 \(\mathcal{X}\)로 표시된다. 두 번째 행에서 크기 STFT가 수정되고(가운데 열이 0으로 설정되어, 신호의 스파이크가 제거됨) 재구성된 신호 \(v_n\) 및 \(x^\mathrm{Rec}\)가 얻어진다. 세 번째 행은 신호 \(x^\mathrm{Rec}\), 윈도우 영역 \(x^\mathrm{Rec}_n\) 및 크기 STFT \(\mathcal{X}^\mathrm{Rec}\)를 보여준다.
Image(path_img+"FMP_C8_F08.png", width=500)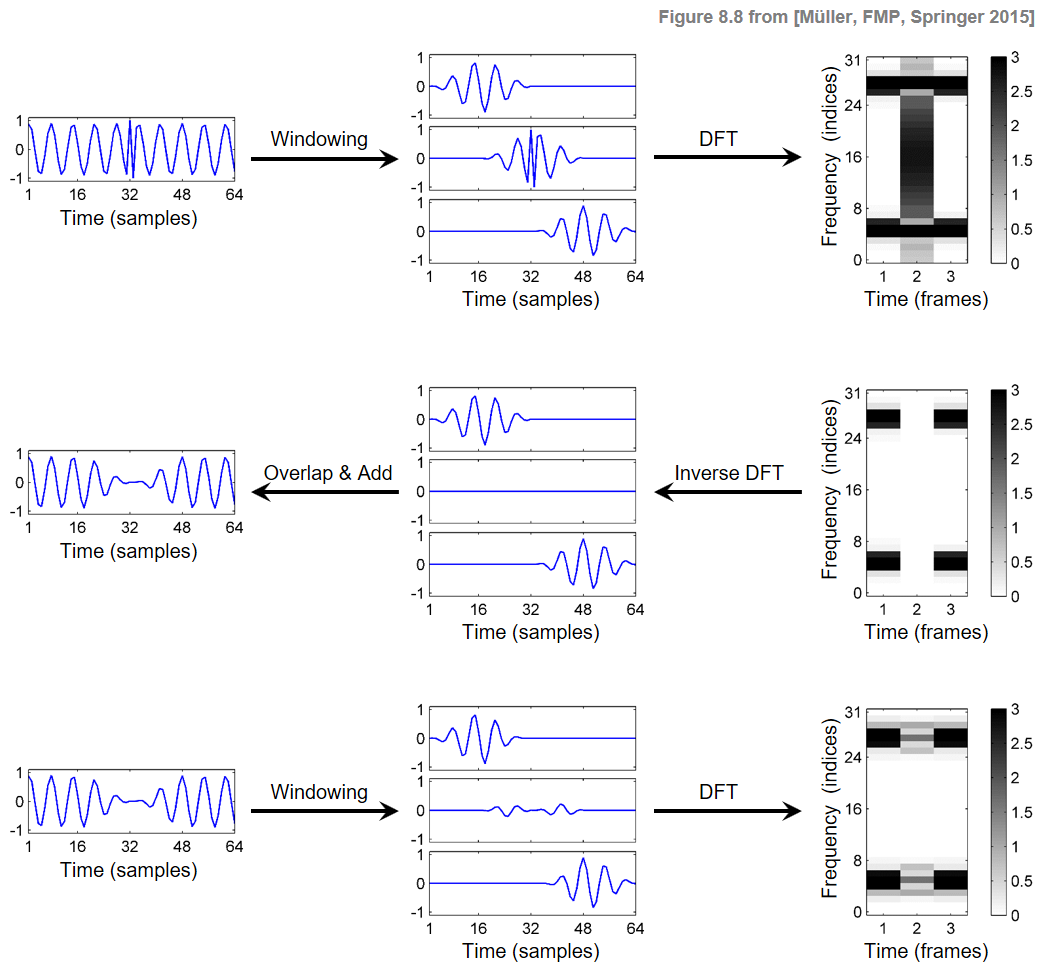
이 그림에서 STFT \(\mathcal{X}^\mathrm{Rec}\)는 MSTFT \(\mathcal{X}^\mathrm{Mod}\)와 일치하지 않는다. 이는 STFT 계산에 사용되는 시간이동된 분석 창이 인접한 창과 겹치기 때문이다. 예를 들어 \(\mathcal{X}^\mathrm{Rec}\)의 두 번째 프레임을 계산하면 첫 번째 및 세 번째 창의 정보도 포함된다.
직관적으로 재구성에서 overlap-add 절차를 사용하면 이전 프레임과 이후 프레임의 정보가 현재 프레임에 재도입된다. \(v_n\) 및 \(x^\mathrm{Rec}_n\) 신호가 다를 수 있지만 이러한 신호에 대한 각각의 합계는 동일한 신호 \(x^\mathrm{Rec}\)를 산출한다.
# Signal
L = 64
t = np.arange(L)/L
omega = 8
x = np.sin(2 * np.pi * omega * t)
x[31] = +1.5
x[32] = -1.5
N = 32
H = N//2
w_type = 'hann'
w = signal.get_window(w_type, N)
X = librosa.stft(x, n_fft=N, hop_length=H, win_length=N, window='hann', pad_mode='constant', center=False)
plt.figure(figsize=(9,2.5))
ax = plt.subplot(1,3,1)
plot_matrix(np.abs(X),ax=[ax],
xlabel='Time (samples)', ylabel='Frequency (bins)',
title=r'STFT $\mathcal{X}$')
X_mod = X
X_mod[:,1]=0
ax = plt.subplot(1,3,2)
plot_matrix(np.abs(X_mod),ax=[ax],
xlabel='Time (frames)', ylabel='Frequency (bins)',
title=r'MSTFT $\mathcal{X}^\mathrm{Mod}$')
x_rec = librosa.istft(X_mod, hop_length=H, win_length=N, window='hann', center=False, length=L)
X_rec = librosa.stft(x_rec, n_fft=N, hop_length=H, win_length=N, window='hann', pad_mode='constant', center=False)
ax = plt.subplot(1,3,3)
plot_matrix(np.abs(X_rec),ax=[ax],
xlabel='Time (frames)', ylabel='Frequency (bins)',
title=r'STFT $\mathcal{X}^\mathrm{Rec}$')
plt.tight_layout()
plt.show()
plt.figure(figsize=(8,2))
plt.subplot(1,2,1)
plt.plot(x, 'k')
plt.xlim([0,L-1])
plt.ylim([-1.6, 1.6])
plt.title(r'Original signal $x$')
plt.xlabel('Time (samples)')
plt.subplot(1,2,2)
plt.plot(x_rec, 'k')
plt.xlim([0,L-1])
plt.ylim([-1.6, 1.6])
plt.title(r'Reconstructed signal $x^\mathrm{Rec}$ from $\mathcal{X}^\mathrm{Mod}$')
plt.xlabel('Time (samples)')
plt.tight_layout()
plt.show()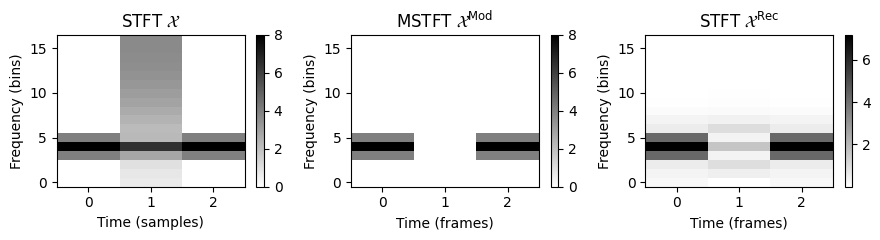
최적화 문제로서의 재구성
재구성된 신호 \(x^\mathrm{Rec}\)의 STFT가 지정된 MSTFT와 일치하지 않을 수 있음을 봤다. 즉 재구성 방법에 관계없이 STFT가 주어진 MSTFT와 일치하는 시간 영역 신호가 존재하지 않을 수 있다.
따라서 적절하게 정의된 거리 측정과 관련하여 STFT가 MSTFT에 가능한 한 근접한 신호를 추정하는 방법을 찾아야 한다.
주어진 MSTFT \(\mathcal{X}^\mathrm{Mod}\)와 신호 \(x'\)의 STFT \(\mathcal{X}'\) 사이의 거리를 측정하기 위해 평균 제곱 오차(mean square error) \(\Delta(\mathcal{X}^\mathrm{Mod},\mathcal{X}')\)를 도입하며 다음과 같이 정의된다. \[\Delta(\mathcal{X}^\mathrm{Mod},\mathcal{X}'):=\sum_{n\in\mathbb{Z}}\,\,\sum_{k\in[0 :N-1]}|\mathcal{X}^\mathrm{Mod}(n,k)-\mathcal{X}'(n,k)|^2.\]
목표는 STFT \(\mathcal{X}^\ast\)가 가능한 모든 신호 \(x'\)에 대해 오차를 최소화하는 신호 \(x^\ast\)를 찾는 것이다. \[x^\ast := \underset{x'}{\mathrm{argmin}} \Delta(\mathcal{X}^\mathrm{Mod},\mathcal{X}')\]
이 최적화 문제는 다음과 같은 방법으로 풀 수 있다. \[x^\ast(r) = \frac{\sum_{n\in\mathbb{Z}} w(r-nH)v_n(r-nH)}{\sum_{n\in\mathbb{Z} } w(r-nH)^2}\]
이 절차는 본질적으로 이전에 설명한 중첩-추가(overlap-add) 기술과 유사하다. 가장 큰 차이점은 최적의 솔루션에서 \(v_n\) 신호가 오버레이 되고 추가되기 전에 분석 윈도우에 표시된다는 것이다. 또한 추가 윈도우잉은 제곱 윈도우의 합으로 정규화하여 보상된다.
자세한 내용과 대체 절차는 Griffin과 Lim의 원본 논문을 참조하자.
- Daniel W. Griffin and Jae S. Lim (1984) “Signal estimation from modified short-time Fourier transform”. IEEE Transactions on Acoustics, Speech, and Signal Processing, 32
HPS, HRPS 적용
- 많은 오디오 처리 작업에서 정보는 오디오 신호의 화성(harmonic) 또는 타악기(percussive) 구성 요소에 있다.
- 예를 들어, 화음 인식(chord recognition)에서 오디오 신호의 화성적 속성을 캡처하고 분류하려고 시도하지만 타악기 속성은 고려하지 않는다.
- 마찬가지로 다성(polyphonic) 음악 녹음에서 메인 멜로디를 결정하려고 할 때 타악기 구성 요소의 존재가 문제가 될 수 있다.
- 다른 작업의 경우 반대 상황이 발생할 수 있다. 예를 들어 드럼 사운드를 분석하고 분류할 때 관련 정보의 대부분은 오디오 신호의 타악기 구성 요소에 포함된다.
- 또한 온셋 감지의 맥락에서 중요한 일시적인 유사 현상의 측정은 음조(tonal) 구성 요소를 사전에 제거할 때 완화될 수 있다.
- 이러한 시나리오는 HP 분리가 다양한 음악 처리 작업을 처리하는 데 유용한 구성 요소가 될 수 있음을 나타낸다.
크로마 특징 향상
첫 번째 예로 HPS 절차의 출력을 사용하여 크로마 기반 오디오 특징(feature)을 향상시키는 방법을 살펴보자. 크로마 특징은 음악의 선율 및 화성 속성이 중요한 작업을 위해 설계되었다. 이러한 특성은 일반적으로 적은 수의 크로마 대역에 신호 에너지가 집중되어 반영된다.
크로마 기반 특징을 계산할 때 스펙트로그램을 피치 하위 밴드으로 분해하는 것으로 시작한다. 이 분해에서 스펙트로그램의 수평 구조는 몇 개의 대역에서 신호 에너지의 높은 집중을 초래하는 반면 수직 구조는 평평한 에너지 분포를 초래한다.
따라서 크로마 표현을 개선하는 한 가지 방법은 먼저 HPS를 적용하여 신호 \(x\)를 하모니 성분 \(x^\mathrm{h}\) 및 타악기 성분 \(x^\mathrm{p}\)로 분해하는 것이다. 그런 다음, 하모니 성분 \(x^\mathrm{h}\)만을 기준으로 크로마 특징을 계산한다. 이러한 HPS 기반 전처리 단계의 효과는 다음 그림에 설명되며, 크기(magnitude) STFT(첫 번째 행)와 원래 신호 \(x\), 하모니 성분 \(x^\mathrm{h}\) 및 타악기 성분 \(x^\mathrm{p}\)에 대한 결과 크로마 표현(두 번째 행)을 보여준다.
# Computation of harmonic and percussive componentn signals
Fs = 11025
#fn_wav = 'FMP_C8_F02_Medi_CastanetsViolin.wav'
fn_wav = 'FMP_C8_F02_Long_CastanetsViolin.wav'
x, Fs = librosa.load(path_data+fn_wav, sr=Fs)
N, H = 512, 256
L_h_sec=0.2
L_p_Hz=500
x_h, x_p = hps(x, Fs=Fs, N=N, H=H, L_h=L_h_sec, L_p=L_p_Hz)# Computation of spectrograms and chromgrams
plt.figure(figsize=(12, 4))
X = librosa.stft(x, n_fft=N, hop_length=H, win_length=N, window='hann', center=True, pad_mode='constant')
Y = np.log(1 + 10 * np.abs(X))
C = librosa.feature.chroma_stft(S=Y, sr=Fs, tuning=0, norm=None, hop_length=H, n_fft=N)
ax = plt.subplot(2,3,1)
plot_matrix(Y, Fs=Fs/H, Fs_F=N/Fs, ax=[ax], title='Mix', clim=[0,5]);
ax = plt.subplot(2,3,4)
plot_chromagram(C, Fs=Fs/H, ax=[ax], clim=[0,70], chroma_yticks=[0,4,7,11]);
X_h = librosa.stft(x_h, n_fft=N, hop_length=H, win_length=N, window='hann', center=True, pad_mode='constant')
Y_h = np.log(1 + 10 * np.abs(X_h))
C_h = librosa.feature.chroma_stft(S=Y_h, sr=Fs, tuning=0, norm=None, hop_length=H, n_fft=N)
ax = plt.subplot(2,3,2)
plot_matrix(Y_h, Fs=Fs/H, Fs_F=N/Fs, ax=[ax], title='Harmonic', clim=[0,5]);
ax = plt.subplot(2,3,5)
plot_chromagram(C_h, Fs=Fs/H, ax=[ax], clim=[0,70], chroma_yticks=[0,4,7,11]);
X_p = librosa.stft(x_p, n_fft=N, hop_length=H, win_length=N, window='hann', center=True, pad_mode='constant')
Y_p = np.log(1 + 10 * np.abs(X_p))
C_p = librosa.feature.chroma_stft(S=Y_p, sr=Fs, tuning=0, norm=None, hop_length=H, n_fft=N)
ax = plt.subplot(2,3,3)
plot_matrix(Y_p, Fs=Fs/H, Fs_F=N/Fs, ax=[ax], title='Percussive', clim=[0,5]);
ax = plt.subplot(2,3,6)
plot_chromagram(C_p, Fs=Fs/H, ax=[ax], clim=[0,70], chroma_yticks=[0,4,7,11]);
plt.tight_layout()
plt.show()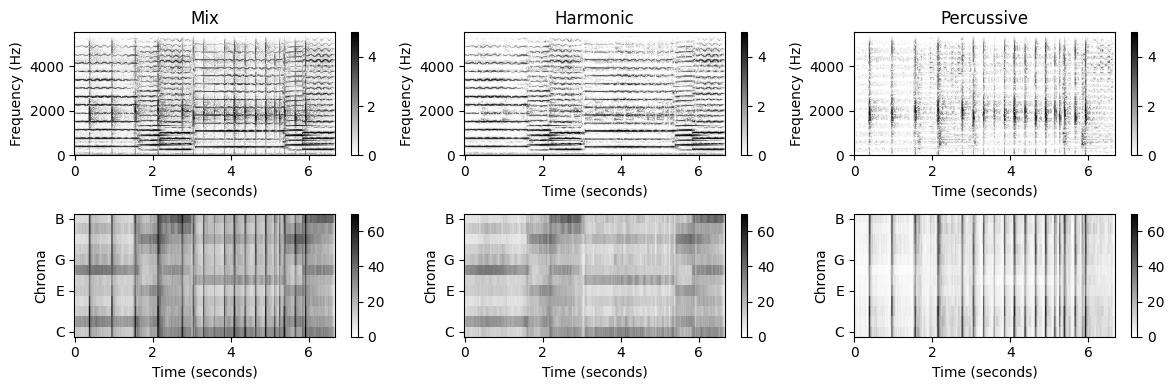
물론, 이 파이프라인에서는 크로마 특징을 계산하기 전에 시간 영역 신호 \(x^\mathrm{h}\)를 재구성할 필요가 없다. 대신, 로그 주파수 및 크로마 표현을 도출하기 위해 마스킹된 크기 STFT \(\mathcal{Y}^\mathrm{h}\)를 직접 사용할 수 있다.
또한 HP 분리 단계는 로그 압축(logarithmic compression) 또는 시간 평활화(temporal smoothing) 와 같은 추가 향상 전략과 쉽게 결합될 수 있다. 그러나 다양한 강화 전략은 서로 영향을 미치거나 유사한 목적을 달성할 수도 있다. 예를 들어 시간적 평활화는 타악기 성분의 영향을 줄이는 것을 목표로 하여 HP 분리 기반 전처리와 유사한 효과를 생성한다.
노벨티 표현 향상
두 번째 예로서 온셋 감지 작업을 고려해 보자.
일반적으로 전체 주파수 스펙트럼에 걸쳐 퍼지는 일시적인 사운드 구성 요소와 함께 온셋 시작이 자주 발생한다. 따라서 HPS 절차는 온셋 감지를 적용하기 전에 수직 시간-주파수 패턴을 향상시키는 데 사용될 수 있다.
다음 예는 이러한 접근 방식의 효과를 보여준다. 여기서 간단한 에너지 기반 참신 함수가 원래 신호뿐만 아니라 하모니 성분 \(x^\mathrm{h}\) 및 타악기 성분 \(x^\mathrm{p}\)에 적용된다.
스펙트럼 변화에 기반한 다른 온셋 감지는 이전의 harmonic-percussive 분해로부터 같은 정도로 이익을 얻지 못할 수 있다. 그 이유는 스펙트럼 변화의 계산이 인접한 스펙트럼 벡터의 열 방향 차이를 고려하여 타악기(수직) 구조의 일부 향상을 이미 포함하고 있기 때문이다.
fig, ax = plt.subplots(2, 4, gridspec_kw={'width_ratios': [1, 1, 1, 0.05],
'height_ratios': [1.5, 1]},
constrained_layout=True, figsize=(12, 4))
# Plotting spectrograms
plot_matrix(Y, Fs=Fs/H, Fs_F=N/Fs, ax=[ax[0,0]], colorbar=None, title='Mix', clim=[0,5]);
plot_matrix(Y_h, Fs=Fs/H, Fs_F=N/Fs, ax=[ax[0,1]], colorbar=None, title='Harmonic', clim=[0,5]);
plot_matrix(Y_p, Fs=Fs/H, Fs_F=N/Fs, ax=[ax[0,2],ax[0,3]], title='Percussive', clim=[0,5]);
# Computation and plotting of novelty curves
N, H = 2048, 256
nov, Fs_nov = compute_novelty_energy(x, Fs=Fs, N=N, H=H)
plot_signal(nov, Fs=Fs_nov, ax=ax[1,0]);
nov, Fs_nov = compute_novelty_energy(x_h, Fs=Fs, N=N, H=H)
plot_signal(nov, Fs=Fs_nov, ax=ax[1,1]);
nov, Fs_nov = compute_novelty_energy(x_p, Fs=Fs, N=N, H=H)
plot_signal(nov, Fs=Fs_nov, ax=ax[1,2]);
ax[1,3].set_axis_off()
plt.show()
시간-척도 수정 향상 (Improving Time-Scale Modification)
Time-scale modification(TSM)은 피치를 변경하지 않고 오디오 신호의 재생 속도를 높이거나 낮추는 작업이다.
음악 신호의 TSM에서 주요 문제는 타악기 트랜지언트(transient) 현상이 종종 지각적으로 저하된다는 것이다. 이러한 저하를 방지하기 위해 일부 TSM 접근 방식은 입력 신호에서 트랜지언트 현상을 명시적으로 식별하고 특수한 방식으로 처리하길 시도한다. 그러나 이러한 접근은 두 가지 이유로 문제가 있다. 첫째, 트랜지언트 감지의 오류는 최종 TSM 결과에 즉각적인 영향을 미치며, 둘째, 트랜지언트의 인지적 보존은 어려운 작업이다.
이 문제를 해결하기 위해 Driedger et al.의 HPS 단계를 적용하여 신호를 화성음 구성 요소와 일반적으로 트랜지언트를 포함하는 타악기 구성 요소로 분할한다. 화성음(하모니) 성분은 큰 프레임 크기를 사용하는 위상 보코더(phase vocoder) 접근 방식으로 수정되는 반면, 노이즈와 같은 타악기 성분은 간단한 시간-영역 중첩-추가 기법(time-domain overlap-add) 으로 수정된다. 명시적인 트랜지언트 감지 없이 트랜지언트를 높은 수준으로 보존하는 짧은 프레임 크기를 사용한다.
다음 그림은 HP 기반 TSM 절차를 보여준다.
Image(path_img+"FMP_C8_F09_TSM.png", width=400)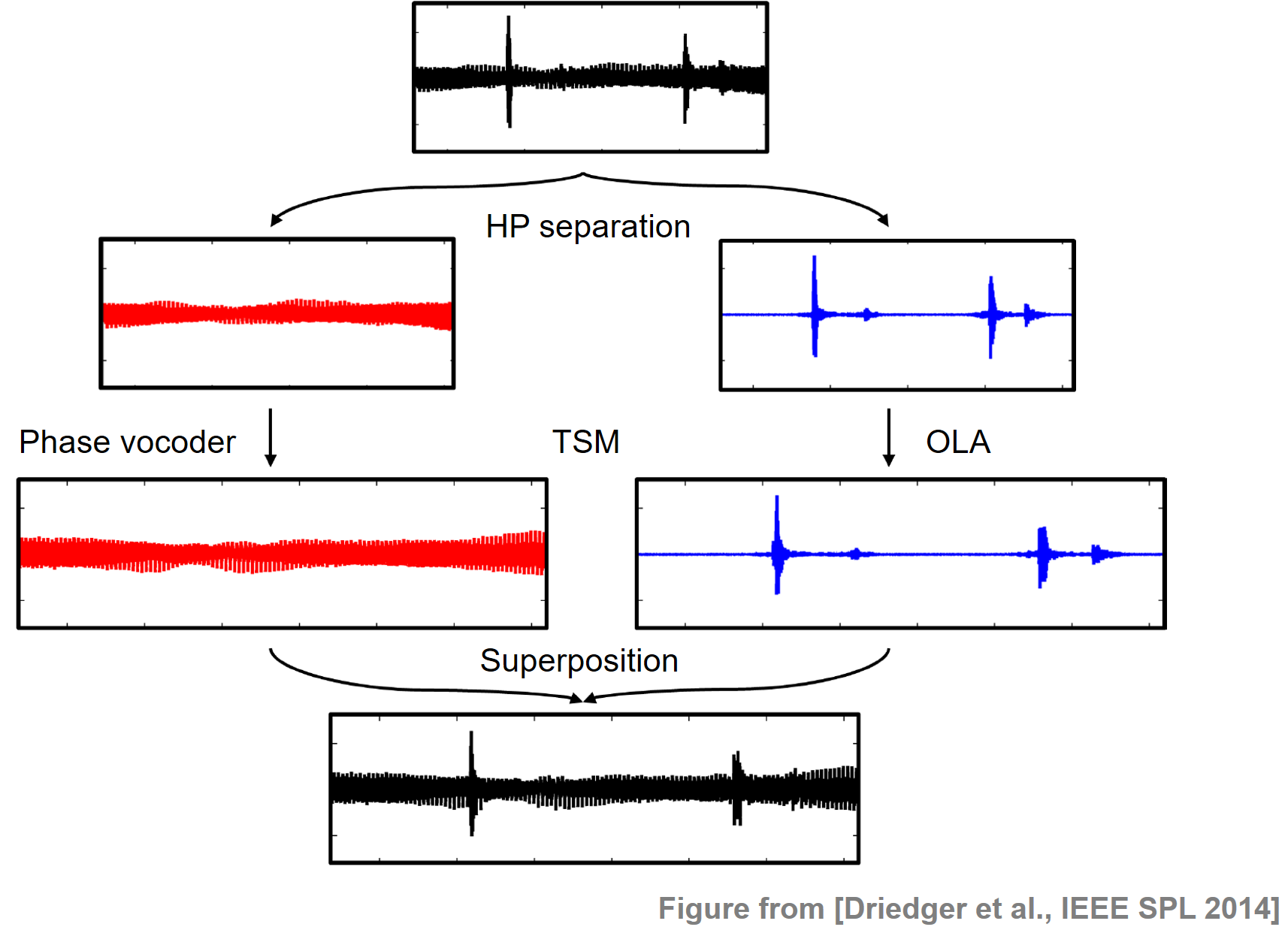
Librosa 간단 예제
xh, sr_h = librosa.load('../audio/prelude_cmaj.wav', duration=7, sr=None)
ipd.Audio(xh, rate=sr_h)xp, sr_p = librosa.load('../audio/125_bounce.wav', duration=7, sr=None)
ipd.Audio(xp, rate=sr_p)# add and rescale
x = xh/xh.max() + xp/xp.max()
x = 0.5 * x/x.max()
x.max()0.5ipd.Audio(x, rate=sr_h)X = librosa.stft(x) # compute stft
Xmag = librosa.amplitude_to_db(np.abs(X)) # take log for display
plt.figure(figsize=(10,3))
librosa.display.specshow(Xmag, sr=sr_h, x_axis='time', y_axis='log')
plt.colorbar()<matplotlib.colorbar.Colorbar at 0x222ea50ac10>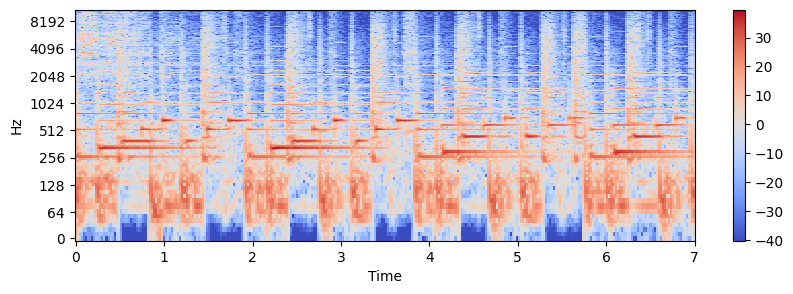
H, P = librosa.decompose.hpss(X) # hpss로 나누기
Hmag = librosa.amplitude_to_db(np.abs(H))
Pmag = librosa.amplitude_to_db(P)
plt.figure(figsize=(10,3))
librosa.display.specshow(Hmag, sr=sr_h, x_axis='time', y_axis='log')
plt.colorbar()<matplotlib.colorbar.Colorbar at 0x222ea540850>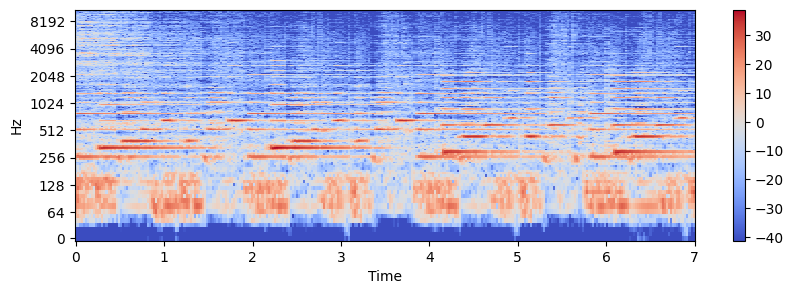
plt.figure(figsize=(10,3))
librosa.display.specshow(Pmag, sr=sr_p, x_axis='time', y_axis='log')
plt.colorbar()<matplotlib.colorbar.Colorbar at 0x222ea580ee0>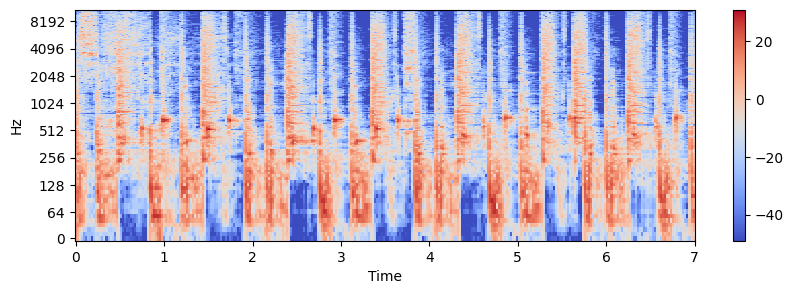
h = librosa.istft(H)
ipd.Audio(h, rate=sr_h)p = librosa.istft(P)
ipd.Audio(p, rate=sr_p)출처:
- https://www.audiolabs-erlangen.de/resources/MIR/FMP/C8/C8S1_HPS.html
- https://www.audiolabs-erlangen.de/resources/MIR/FMP/C8/C8S1_HRPS.html
- https://www.audiolabs-erlangen.de/resources/MIR/FMP/C8/C8S1_SignalReconstruction.html
- https://www.audiolabs-erlangen.de/resources/MIR/FMP/C8/C8S1_HPS-Application.html
- https://colab.research.google.com/github/stevetjoa/musicinformationretrieval.com/blob/gh-pages/hpss.ipynb
\(\leftarrow\) 8.4. 버전 식별