import numpy as np
import scipy
from scipy import signal
from matplotlib import pyplot as plt
import matplotlib.gridspec as gridspec
from matplotlib.colors import ListedColormap
import IPython.display as ipd
import pandas as pd
import librosa, librosa.display
from utils.feature_tools import normalize_feature_sequence, smooth_downsample_feature_sequence, median_downsample_feature_sequence
from utils.plot_tools import plot_matrix, compressed_gray_cmap, plot_chromagram, plot_segments
import utils.tempo_tools as tmpo
from utils.structure_tools import read_structure_annotation, convert_structure_annotation5.2. 자기 유사성 행렬 (SSM)
Self Similarity Matrix
음악 구조를 분석하기 위한 기술적 도구인 자기 유사성 행렬(self similarity matrix)의 개념에 대해 상세히 다루고, 그 구조적 속성에 대해 논의한다.
이 글은 FMP(Fundamentals of Music Processing) Notebooks을 참고로 합니다.
자기 유사성 행렬 (Self Similarity Matrix, SSM)
기본 정의
- \(\mathcal{F}\)를 특징(feature) 공간이라고 하고 \(s:\mathcal{F}\times\mathcal{F}\to \mathbb{R}\)를 두 요소 \(x,y\in\mathcal{F}\)를 비교할 수 있는 유사성(similarity) 척도라고 하자. 일반적으로 \(s(x,y)\) 값은 요소 \(x,y\in\mathcal{F}\)가 비슷하면 높고 그렇지 않으면 작다.
- 특징 시퀀스 \(X=(x_1,x_2,\ldots,x_N)\)가 주어지면 시퀀스의 모든 요소를 서로 비교할 수 있다.
- 결과적으로 \(N\)-square 자기 유사성 행렬(self-similarity matrix) \(\mathbf{S}\in\mathbb{R}^{N\times N}\)이 아래와 같이 정의된다.
\[\mathbf{S}(n,m):=s(x_n,x_m),\] where \(x_n,x_m\in\mathcal{F}\) for \(n,m\in[1:N]\)
다음에서 \((n,m)\in[1:N]\times[1:N]\) 튜플은 \(\mathbf{S}\)의 셀(cell)이라고도 하며 값 \(\mathbf{S}(n,m)\)는 셀 \((n,m)\)의 점수(score)라고 한다.
응용의 맥락 및 데이터를 비교하는 데 사용되는 개념에 따라 반복 플롯(recurrence plot), 비용 매트릭스(cost matrix) 또는 자기-거리 매트릭스(self-distance matrix) 와 같은 다른 이름으로 알려진 관련된 개념이 많다.
종종 특징 공간이 차원 \(K\in\mathbb{N}\)의 유클리드 공간 \(\mathcal{F}=\mathbb{R}^K\)라고 가정한다. 간단한 유사성 측정 \(s\)는 예를 들어 다음과 같이 정의된 내적이다.
\[s(x,y) := \langle x,y\rangle\] for two vectors \(x,y\in\mathcal{F}\)
이 유사성 측정을 사용하면 직교(orthogonal)하는 두 특징(feature) 벡터 사이의 점수는 0이고, 그렇지 않으면 0이 아니다. 특징 벡터가 유클리드 노름(norm)에 대해 정규화되는 경우, 유사성 값 \(s(x,y)\)는 \([-1,1]\) 구간에 있다. 이 경우 정규화된 피쳐의 시퀀스 \(X=x_1,x_2,\ldots,x_N)\)가 주어지면, \(s(x_n,x_n)=1\) for all \(n\in[1:N]\)인 경우 SSM의 최대값이 가정된다. 따라서 결과 SSM에는 값이 큰 대각선이 있다. 더 일반적으로 말하면, 주어진 특징 시퀀스의 반복 패턴은 유사성 값이 큰 구조의 형태로 SSM에서 볼 수 있다.
다음 예에서는 정규화된(normalized) 특징 벡터의 합성(synthetic) 특징 시퀀스를 생성한다. 특징 벡터의 차원은 \(K=4\)이고 시퀀스의 길이는 \(N=500\)이다. 그림은 특징 시퀀스와 결과 SSM을 보여준다.
중요 사항:
- SSM을 시각화할 때 컬러맵 ’cmap’의 선택은 그림의 전체적인 모습에 상당한 영향을 미칠 수 있다. 적합한 컬러맵을 선택하면 SSM의 특정 속성을 시각적으로 강조하는 데 도움이 될 수 있다.
- 위에서 설명한 정규화된 특징의 특징 시퀀스와 유사도 측정을 사용하면 간단한 행렬-행렬 곱으로 SSM을 계산할 수 있다. 보다 정확하게는 \(K\times N\)-matrix \(X\)에 의해 특성 시퀀스가 구현되는 경우, SSM \(S\)는 \(S=X^\top X\)로 주어진다.
- 또한, 특징 벡터의 모든 항목이 양수라고 종종 가정한다. 이 경우 \(s(x_n,x_m)\) 값은 양수이며 \([0,1]\) 간격에 있다.
# Generate normalized feature sequence
K = 4
M = 100
r = np.arange(M)
b1 = np.zeros((K,M))
b1[0,:] = r
b1[1,:] = M-r
b2 = np.ones((K,M))
X = np.concatenate(( b1, b1, np.roll(b1, 2, axis=0), b2, b1 ), axis=1)
X_norm = normalize_feature_sequence(X, norm='2', threshold=0.001)
# Compute SSM
S = np.dot(np.transpose(X_norm), X_norm)
# Visualization
cmap = 'gray_r'
fig, ax = plt.subplots(2, 2, gridspec_kw={'width_ratios': [1, 0.05],
'height_ratios': [0.3, 1]}, figsize=(4, 5))
plot_matrix(X_norm, Fs=1, ax=[ax[0,0], ax[0,1]], cmap=cmap,
xlabel='Time (frames)', ylabel='', title='Feature sequence')
plot_matrix(S, Fs=1, ax=[ax[1,0], ax[1,1]], cmap=cmap,
title='SSM', xlabel='Time (frames)', ylabel='Time (frames)', colorbar=True);
plt.tight_layout()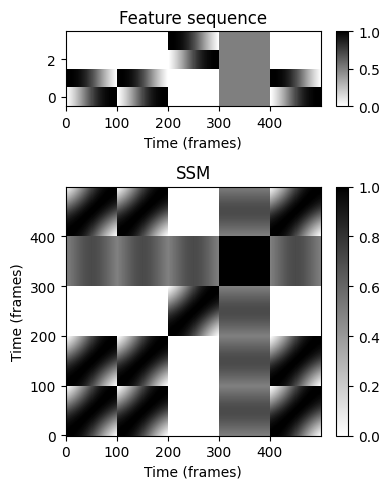
- 컬러맵을 적절하게 조정하여 시각적 모양을 변경할 수 있다. 예를 들어 색상 분포를 더 밝은 색상으로 이동하면 시각화의 경로 구조가 향상된다.
cmap = compressed_gray_cmap(alpha=-1000)
fig, ax = plt.subplots(2, 2, gridspec_kw={'width_ratios': [1, 0.05],
'height_ratios': [0.3, 1]}, figsize=(4,5))
plot_matrix(X, Fs=1, ax=[ax[0,0], ax[0,1]], cmap=cmap,
xlabel='Time (frames)', ylabel='', title='Feature sequence')
plot_matrix(S, Fs=1, ax=[ax[1,0], ax[1,1]], cmap=cmap,
title='SSM', xlabel='Time (frames)', ylabel='Time (frames)', colorbar=True);
plt.tight_layout()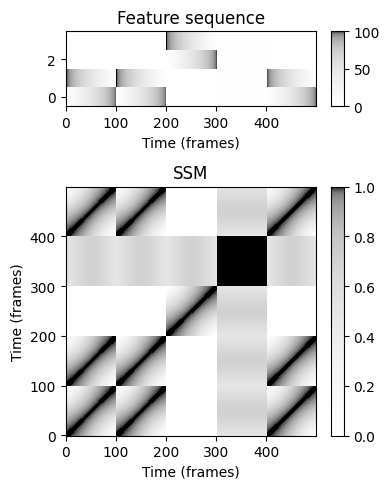
블록과 경로구조 (Block and Path Structures)
SSM에서 가장 눈에 띄는 두 가지 구조는 이미 앞의 예에서 볼 수 있듯이 블록(block) 및 경로(paths) 라고 한다.
특징 시퀀스가 전체 음악의 지속 기간(duration) 동안 다소 일정하게 유지되는 음악 속성을 캡처하는 경우, 각 특징 벡터는 이 세그먼트 내의 다른 모든 특징 벡터와 유사함을 의미한다. 결과적으로 큰 값의 전체 블록이 SSM에 나타난다.
- 즉, 동질성(homogeneity) 속성은 블록 같은(block-like) 구조에 해당한다.
특징 시퀀스가 2개의 반복 하위시퀀스(예를 들어, 동일한 멜로디에 대응하는 2개의 세그먼트)를 포함하는 경우, 두 하위시퀀스의 대응하는 요소는 서로 유사하다. 결과적으로 주 대각선과 평행하게 실행되는 유사성이 높은 경로(또는 스트라이프(stripe))가 SSM에 표시된다.
- 즉, 반복(repetitive) 속성은 경로 같은(path-like) 구조에 해당한다.
예로, 다음 그림은 음악적 구조가 \(A_1A_2B_1B_2CA_3B_3B_4D\)인 Brahms의 헝가리 무곡 5번에 대한 이상적인 SSM을 보여준다. 세 개의 반복되는 \(A\) 부분 세그먼트가 동종이라고 가정하면 SSM에는 \(A_1A_2\)에 해당하는 세그먼트를 자신과 관련시키는 2차 블록과 \(A_3\) 부분 세그먼트를 자신과 관련시키는 또 다른 2차 블록이 있다. 또한 두 개의 직사각형 블록이 있는데, 하나는 \(A_1A_2\) 부분 세그먼트를 \(A_3\) 부분 세그먼트에 연결하고 다른 하나는 \(A_3\) 부분 세그먼트를 \(A_1A_2\) 부분 세그먼트에 연결한다. 3개의 반복되는 \(A\) 부분 세그먼트가 동질적이지 않은 경우 SSM은 주 대각선에 평행하게 실행되는 경로 구조를 나타낸다. 예를 들어 \(A_1\)와 \(A_2\)의 유사도가 큰 경로와 \(A_1\)와 \(A_3\)의 경로가 있다.
ipd.Image("../img/5.music_structure_analysis/FMP_C4_F07a.png", width=300)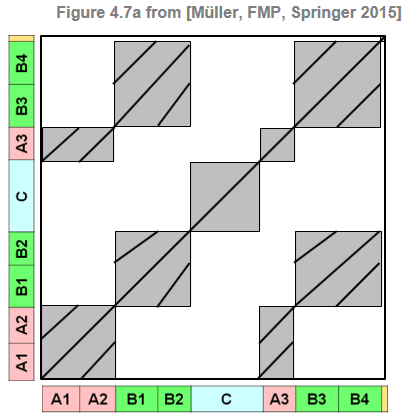
크로마그램 기반 SSM
- 다음 코드는 크로마그램(chromagram) 을 특징 표현으로 사용하여 Brahms의 헝가리 댄스 녹음에서 SSM을 생성한다. 시각화에서 \(\mathbf{S}\)의 큰 값은 어두운 회색으로 표시되고 작은 값은 밝은 회색으로 표시된다.
- 실제로 이 경우 얻은 SSM은 이상적인 SSM과 상당 부분 유사하다. \(A\) 부분 세그먼트에 해당하는 block-like 구조는 이러한 세그먼트가 화음과 관련하여 상당히 동질적임을 나타낸다. \(C\) 부분 세그먼트도 마찬가지다. 또한, \(C\) 부분 블록 외부의 작은 유사성 값(즉, \(C\) 부분 프레임을 다른 세그먼트의 프레임에 연결하는 모든 셀)은 \(C\) 부분 세그먼트가 화성적으로 모든 부분과 거의 관련이 없음을 보여준다. \(B\) 부분 세그먼트의 경우 path-like 구조가 있고 block-like 구조는 없다. 이는 \(B\) 파트 세그먼트가 동일한 화성 진행(즉, 화성에 대한 반복)을 공유하지만 화성에 대해 동질적이지 않음을 보여준다.
- 흥미로운 점은 반복하더라도 \(B\) 부분 세그먼트가 다른 템포로 재생되므로 길이가 다르다는 것이다. 예를 들어 짧은 \(B_2\) 섹션은 \(B_1\) 섹션보다 빠르게 재생된다. 결과적으로 해당 경로는 정확히 병렬로 실행되지 않는다.
def compute_sm_dot(X, Y):
"""Computes similarty matrix from feature sequences using dot (inner) product
Args:
X (np.ndarray): First sequence
Y (np.ndarray): Second Sequence
Returns:
S (float): Dot product
"""
S = np.dot(np.transpose(X), Y)
return Sdef plot_feature_ssm(X, Fs_X, S, Fs_S, ann, duration, color_ann=None,
title='', label='Time (seconds)', time=True,
figsize=(5, 6), fontsize=10, clim_X=None, clim=None):
"""Plot SSM along with feature representation and annotations (standard setting is time in seconds)
Args:
X: Feature representation
Fs_X: Feature rate of ``X``
S: Similarity matrix (SM)
Fs_S: Feature rate of ``S``
ann: Annotaions
duration: Duration
color_ann: Color annotations (see :func:`libfmp.b.b_plot.plot_segments`) (Default value = None)
title: Figure title (Default value = '')
label: Label for time axes (Default value = 'Time (seconds)')
time: Display time axis ticks or not (Default value = True)
figsize: Figure size (Default value = (5, 6))
fontsize: Font size (Default value = 10)
clim_X: Color limits for matrix X (Default value = None)
clim: Color limits for matrix ``S`` (Default value = None)
Returns:
fig: Handle for figure
ax: Handle for axes
"""
cmap = compressed_gray_cmap(alpha=-10)
fig, ax = plt.subplots(3, 3, gridspec_kw={'width_ratios': [0.1, 1, 0.05],
'wspace': 0.2,
'height_ratios': [0.3, 1, 0.1]},
figsize=figsize)
plot_matrix(X, Fs=Fs_X, ax=[ax[0, 1], ax[0, 2]], clim=clim_X,
xlabel='', ylabel='', title=title)
ax[0, 0].axis('off')
plot_matrix(S, Fs=Fs_S, ax=[ax[1, 1], ax[1, 2]], cmap=cmap, clim=clim,
title='', xlabel='', ylabel='', colorbar=True)
ax[1, 1].set_xticks([])
ax[1, 1].set_yticks([])
plot_segments(ann, ax=ax[2, 1], time_axis=time, fontsize=fontsize,
colors=color_ann,
time_label=label, time_max=duration*Fs_X)
ax[2, 2].axis('off')
ax[2, 0].axis('off')
plot_segments(ann, ax=ax[1, 0], time_axis=time, fontsize=fontsize,
direction='vertical', colors=color_ann,
time_label=label, time_max=duration*Fs_X)
return fig, axfn_wav = '../data_FMP/FMP_C4_Audio_Brahms_HungarianDances-05_Ormandy.wav'
x, Fs = librosa.load(fn_wav)
ipd.Audio(x,rate=Fs)