AI 연구는 확률, 통계에 대한 기초적인 지식을 필요로 한다. 하지만, 확률, 통계를 공부했다고 하더라도, 잠시 관심을 꺼둔다면, 기초적인 지식조차도 금방 잊어버리기 마련이다. 필요할 때마다 찾아볼 수 있도록, 확률, 통계에 대한 간단한 기본 지식을 정리했다.
확률 분포
확률 분포는 특정 사건이 발생할 가능성을 설명하는 수학적 모델
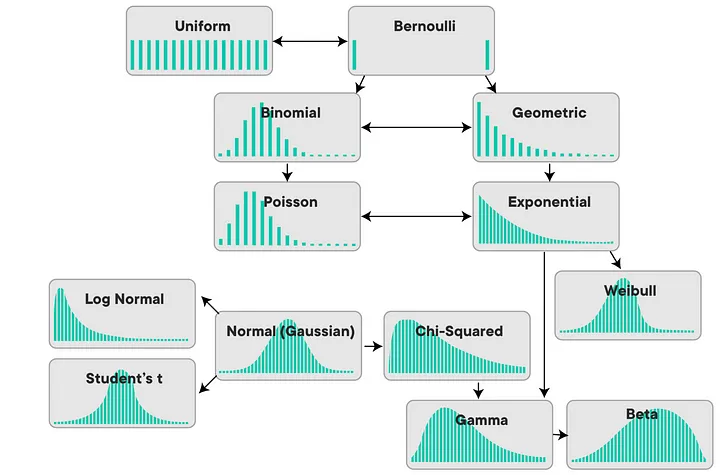
이산 확률 분포 (Discrete probability distributions)
Bernouille distribution
- 단일 시행에서 두 가지 결과(성공 1 /실패 0) 실험 모델링
- 예: 동전 한번 던지기
\(P(X=k) = p^k (1-p)^{1-k} \quad \text{for} \ k \in \{0,1\}\)
\(E(x) = p\)
\(V(x) = p(1-p)\)
Binomial distribution
- 고정된 수(\(n\))의 독립 시행에서 성공 횟수(\(k\))의 분포 (즉, 여러 베르누이 시행)
- 사용 예시: 동전 던지기
\(P(X=k) = \binom{n}{k} p^k (1-p)^{n-k}\)
\(E(x) = np\)
\(V(x) = np(1-p)\)
Poisson distribution

- 단위 시간 또는 공간에서 발생하는 사건의 수
- 한 시간 동안의 전화 통화 횟수(\(k\))
\(P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}\)
\(P(X \leq K) = 1 - \sum^{K}_{k=0}\frac{\lambda^k e^{-\lambda}}{k!}\)
\(E(x) = \lambda\)
\(V(x) = \lambda\)
Negative binomial distribution

- 베르누이 시행에서 성공 \(r\)회가 나타나기까지의 실패 횟수를 모델링
- 팀이 \(r\)개의 중대한 버그를 모두 수정하기까지, 몇 번의 코드 검토가 필요할지 추정
\(P(X = k) = \binom{k + r - 1}{k} (1-p)^k p^r\)
\(E(X) = \frac{r(1-p)}{p}\)
\(V(X) = \frac{r(1-p)}{p^2}\)
Hypergeometric distribution
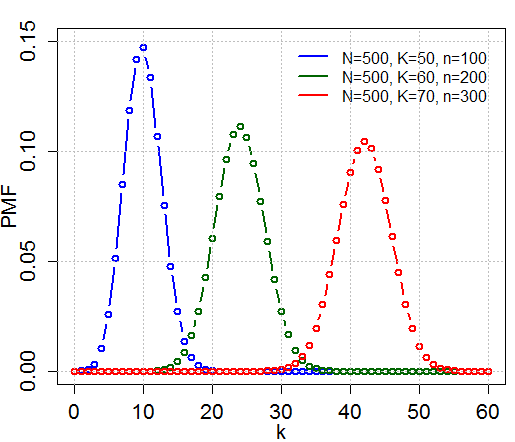
- 한정된 특정 수(\(N\))의 모집단에서 교체없이(without replacement) 특정 성공 사건이 몇 번 발생했는지 모델링
- 예시, \(N\)개 카드 덱(\(K\)개 하트카드)에서 한번에 \(n\)개 카드을 뽑았을 때, 뽑은 카드 중 \(k\)개가 하트 카드일 확률 계산
\(P(X = k) = \frac{{\binom{K}{k}}{\binom{N-K}{n-k}}}{\binom{N}{n}}\)
\(F(x) = 1 - (1-p)^{x} \quad \text{for} \ x \geq 1\)
\(E(X) = n\frac{K}{N}\)
\(V(X) = n\frac{K}{N}\frac{N-K}{N}\frac{N-n}{N-1}\)
Geometric distribution

- 베르누이 시행에서 처음 성공까지 시도한 횟수 \(X\)의 분포
- 예시: 동전 앞면이 나올 때까지 동전 던진 횟수(\(k\))
\(P(X=k) = (1-p)^{k-1}p\)
\(F(x) = 1 - (1-p)^{x} \quad \text{for} \ x \geq 1\)
\(E(x) = \frac{1}{p}\)
\(V(x) = \frac{1-p}{p^2}\)
연속확률분포 (Continuous probability distributions)
Normal distribution
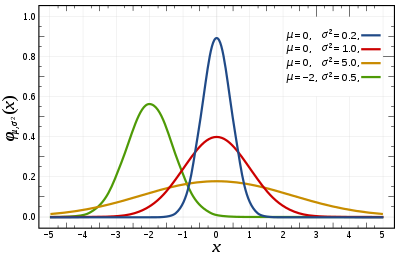
- 자연 현상에서 발생하는 많은 데이터의 분포를 모델링 (aka 가우시안 분포)
- 인간의 키나 몸무게
\(f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)
\(F(x|\mu,\sigma) = \frac{1}{2} \left[1 + \text{erf}\left(\frac{x-\mu}{\sigma\sqrt{2}}\right)\right]\), \(\text{erf}(z) = \frac{2}{\sqrt{\pi}} \int_{0}^{z} e^{-t^2} dt\)
\(E(x) = \mu\)
\(V(x) = \sigma^2\)
Student’t t-distribution
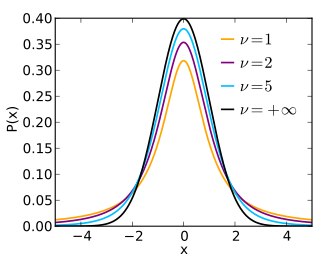
- 작은 표본 크기에서 정규 분포의 평균을 추정할 때 사용되는 분포
- t 검정, 신뢰 구간 추정
\(f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)
\(F(x|\mu,\sigma) = \frac{1}{2} \left[1 + \text{erf}\left(\frac{x-\mu}{\sigma\sqrt{2}}\right)\right]\), \(\text{erf}(z) = \frac{2}{\sqrt{\pi}} \int_{0}^{z} e^{-t^2} dt\)
\(E(x) = \mu\)
\(V(x) = \sigma^2\)
Chi-squared Distribution

- 독립적인 표준 정규 분포를 따르는 변수들의 제곱 합의 분포
- 사용 예시: 분산 분석, 카이제곱 검정 (적합도 검정, 독립성 검정) 등
\(f(x; k) = \frac{1}{2^{\frac{k}{2}}\Gamma\left(\frac{k}{2}\right)}x^{\frac{k}{2}-1}e^{-\frac{x}{2}}\)
\(E(x) = k\)
\(V(x) = 2k\)
Exponential distribution

- 일정한 평균 속도(\(\lambda\))로 발생하는 독립적인 사건 사이의 시간을 모델링
- 예시: 기계가 고장 나기까지의 시간
\(f(x) = \lambda e^{-\lambda x}\)
\(F(x) = 1 - e^{-\lambda x} \quad \text{for} \ x \geq 0\)
\(E(x) = \frac{1}{\lambda}\)
\(V(x) = \frac{1}{\lambda^2}\)
Weibul distribution
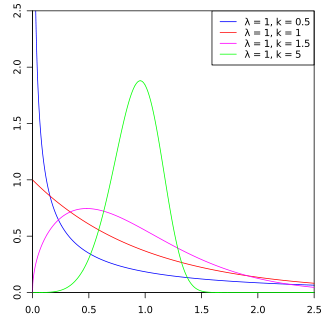
- 모양 매개변수(\(\lambda\))와 스케일 매개변수(\(k\))에 의해 정의
- 예시: 제품의 수명, 재료의 파손 시간, 또는 대기 시간 분석 등
\(f(x) = \frac{k}{\lambda} \left( \frac{x}{\lambda} \right)^{k - 1} e^{-(x/\lambda)^k}\)
\(F(x) = 1 - e^{-(x/\lambda)^k}\)
\(E(x) = \lambda \Gamma\left(1 + \frac{1}{k}\right)\)
\(V(x) = \lambda^2 \left[ \Gamma\left(1 + \frac{2}{k}\right) - \left(\Gamma\left(1 + \frac{1}{k}\right)\right)^2 \right]\)
Gamma Distribution
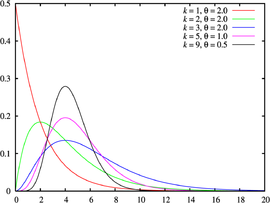
- 지수분포에서 한 번의 사건이 아닌 여러 개의 사건으로 확장
- \(\alpha\)번째 사건이 발생할때까지 걸리는 시간이 \(T\)이하일 확률
- 사용 예시: 여러 기계의 수명 합, 모수의 베이지안 추정
\(f(x) = \frac{x^{\alpha-1}e^{-x/\beta}}{\Gamma(\alpha)\beta^\alpha} \quad \text{for } x > 0\)
\(E(x) = \alpha\beta\)
\(V(x) = \alpha\beta^2\)
Beta Distribution

- 0과 1 사이의 값에 대한 확률 분포로, 성공 확률의 불확실성을 모델링할 때 사용
- 두 매개변수 \(\alpha, \beta\)에 의해 모양이 결정되며, 이 매개변수들은 분포의 모양을 조절하는 데 사용
- 사용 예시: 베이지안 통계에서 사전 분포(prior distribution), A/B 테스트 결과의 해석 등
\(f(x;\alpha,\beta) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)}\)
\(B(\alpha, \beta) = \int_{0}^{1} t^{\alpha-1}(1-t)^{\beta-1} dt\) (베타함수)
\(E(x) = \frac{\alpha}{\alpha + \beta}\)
\(V(x) = \frac{\alpha\beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}\)
적률
적률(moments)이란
k차 원점 적률: \(\mu'_k = \int_{-\infty}^{\infty} x^k f(x) dx = E[X^k]\)
k차 중심 적률: \(\mu_k = \int_{-\infty}^{\infty} (x-\mu)^k f(x) dx = E[(X-\mu)^k]\)
k차 표준화 적률: \(\tilde{\mu}_k = \frac{\mu_k}{\sigma^k} = E[{(\frac{X-\mu}{\sigma})}^k]\)
평균, 분산, 왜도, 첨도
1차 원점 적률(평균): 데이터의 평균 값을 나타냄 \(\mu = E[X]\)
1차 중심 적률: 0
2차 중심 적률(분산): 데이터의 분산을 나타냄 \(E[(X-\mu)^2]\)
3차 중심 표준화 적률(왜도): 데이터 분포의 비대칭도를 나타냄 \(E[{(\frac{X-\mu}{\sigma})}^3]\)
4차 중심 표준화 적률(첨도): 데이터 분포의 뾰족함을 나타냄 \(E[{(\frac{X-\mu}{\sigma})}^4]\)
적률 생성 함수(MGF)
적률 생성 함수는 확률변수의 모든 적률을 유도하기 위한 방법으로 사용
\[M_X(t) = E[e^{tX}] = \int_{-\infty}^{\infty} e^{tx} f(x) dx\]
이때, 확률변수 \(X\)의 \(n\)번째 적률은 \(M(t)\)를 \(t\)에 대해 \(n\)번 미분하고 \(t=0\)을 대입하여 얻을 수 있음
\[\mu_n' = E[X^n] = \left. \frac{d^n M(t)}{dt^n} \right|_{t=0}\]
\(e^{tX}\)를 테일러 전개하여, 적률 생성 함수에 대입하면,
\(M_X(t) = E[e^{tX}] = E\left[1 + Xt + \frac{X^2t^2}{2!} + \frac{X^3t^3}{3!} + \ldots \right]\)
\(M_X(t) = E[e^{tX}] = 1 + E[X]t + \frac{E[X^2]t^2}{2!} + \frac{E[X^3]t^3}{3!} + \ldots\)
\(n\)차 미분하여 \(t=0\)을 대입하면, \(n\)차 적률이 되는 것을 알 수 있다.
적률 생성 함수의 특징
- 존재성: 모든 적률이 존재하는 확률변수는 MGF가 적어도 \(t=0\)을 중심으로 한 작은 주변에서 존재
- 유일성: 두 확률변수의 MGF가 존재하고 같다면, 그 확률변수들은 동일한 확률분포를 가짐
- 선형성: 확률변수 \(X\)와 \(Y\)가 독립이고 \(M_X(t)\), \(M_Y(t)\)의 MGF를 가진다면 \(X+Y\)의 MGF는 \(M_X(t) \times M_Y(t)\)
정규분포의 적률생성함수
- \(M_X(t) = \int_{-\infty}^{\infty} e^{tx} \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} dx\)
- \(...\)
- \(M_X(t) = e^{\mu t + \frac{1}{2}\sigma^2 t^2}\)
엔트로피
엔트로피(entropy)란
엔트로피(entropy)는 확률분포가 가지는 정보의 확신도 혹은 정보량을 수치로 표현한 것이다. 확률분포에서 특정한 값이 나올 확률이 높아지고 나머지 값의 확률은 낮아진다면 엔트로피가 작아진다.
지니 불순도(gini impurity)
지니 불순도(Gini impurity)는 데이터 집합 내에서 랜덤으로 선택한 요소가 잘못 분류될 확률을 측정, 주어진 데이터 집합이 얼마나 “혼합”되어 있는지를 나타냄
\[G(Y) = \sum_{k=1}^{K} P(y_k) (1 - P(y_k))\]
# 예시: 베르누이 분포의 엔트로피, 지니 불순도
import numpy as np
import matplotlib.pyplot as plt
P0 = np.linspace(0.001, 1 - 0.001, 1000)
P1 = 1 - P0
H = - P0 * np.log2(P0) - P1 * np.log2(P1)
G = 2 * (P0 * (1 - P0) + P1 * (1 - P1))
plt.plot(P1, H, "-", label="entropy")
plt.plot(P1, G, "--", label="gini")
plt.legend()
plt.xlabel("P(Y=1)")
plt.show()
크로스-엔트로피
크로스-엔트로피(cross-entropy)는 두 확률분포 간의 차이를 측정하는 데 사용
Cross-entropy는 머신러닝과 딥러닝에서 손실 함수(loss function)로 널리 사용되며, 특히 분류 문제에서 예측 분포 \(Q\)가 실제 분포 \(P\)를 얼마나 잘 추정하는지를 평가할 때 중요함
이때 낮은 cross-entropy 값은 모델의 예측이 실제 분포에 더 가깝다는 것을 의미
\(H(P, Q) = -\sum_{x} P(x) \log Q(x)\) (이산)
\(H(P, Q) = -\int p(x) \log q(x) \, dx\) (연속)
참고자료
- Wikipedia(https://www.wikipedia.org/)











